图

图的定义

图 $G$ 由顶点集 $V$ 和边集 $E$ 组成，记为 $G = (V, E)$，其中 $V(G)$ 表示图 $G$ 中顶点的有限非空集，$E(G)$ 表示图 $G$ 中顶点之间的关系（边）集合。若 $V = \{v_1, v_2, \ldots, v_n\}$，则用 $|V|$ 表示图 $G$ 中顶点的个数（称为图的阶），$E = \{(u, v) \mid u \in V, v \in V\}$，用 $|E|$ 表示图 $G$ 中边的条数。

线性表可以是空表，树可以是空树，但是图不能是空图，即使他没有边，他也不能没有顶点，也就是说图中不能一个定点都没有，但边集E可以为空。
G:Graph V:Vertex E:Edge

来点题外话：假设南昌东站、昌北机场站、共青城东站、庐山东站是一个个顶点V，那么连接他们之间的铁路可以看作是边E，那么构成的图G就是一张图。也就是京港高铁昌九段，在延申一点就是全国高铁网络均可看作是一张大图。

有关图的相关概念

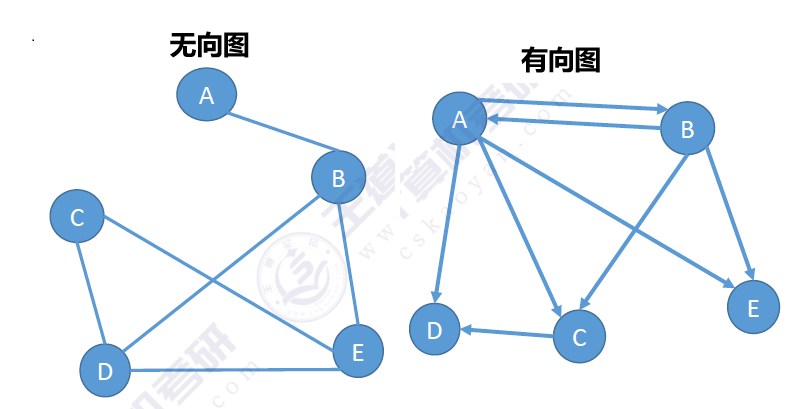
有向图和无向图

有向图：若 $E$ 是有向边（弧）的有限集合，则图 $G$ 为有向图。弧是顶点的有序对，记为 $\langle v, w \rangle$，其中 $v$、$w$ 是顶点，$v$ 称为弧尾，$w$ 称为弧头，$\langle v, w \rangle$ 表示从顶点 $v$ 到顶点 $w$ 的弧。$\langle v, w \rangle \ne \langle w, v \rangle$。
无向图：若 $E$ 是无向边（边）的有限集合，则图 $G$ 为无向图。无向边是顶点的无序对，记为 $(v, w)$ 或 $(w, v)$，其中 $v$、$w$ 是顶点，且 $(v, w) = (w, v)$。

示例：

有向图 $G_1 = (V_1, E_1)$
$V_1 = \{A, B, C, D, E\}$
$E_1 = \{\langle A, B \rangle, \langle A, C \rangle, \langle A, D \rangle, \langle A, E \rangle, \langle B, A \rangle, \langle B, C \rangle, \langle B, E \rangle, \langle C, D \rangle\}$

无向图 $G_2 = (V_2, E_2)$
$V_2 = \{A, B, C, D, E\}$
$E_2 = \{(A, B), (B, D), (B, E), (C, D), (C, E), (D, E)\}$

有向图无向图示例

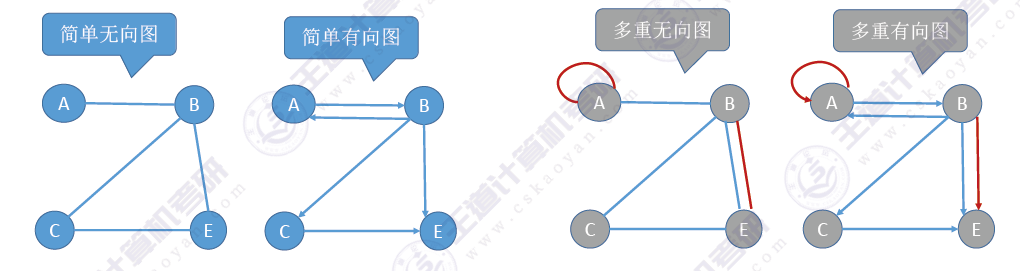
简单图和多重图

简单图：满足不存在重复边，不存在顶点到自身的边。数据结构只讨论简单图。
多重图：两个结点的边数多余一条，且允许有顶点到自身的边。与简单图相对。

简单图/多重图

顶点的度

无向图

顶点的度：一个顶点的度等于依附于该顶点的边的条数。记作$TD(v)$
所有顶点的度之和等于边数的两倍。
在具有n个顶点，e条边的无向图图，$\sum^n_{i=1}TD(v_i)=2e$

有向图

入度：以该顶点为终点的有向边的条数。记作$ID(v)$
出度：以该顶点为起点的有向边的条数。记作$OD(v)$
顶点的度 = 入度 + 出度。$TD(v)=ID(v)+OD(v)$
所有顶点的入度之和等于所有顶点的出度之和，且都等于边的总数。
在具有n个顶点，e条边的有向图，$\sum^n_{i=1}ID(v_i)=\sum^n_{i=1}OD(v_i)=e$

顶点之间的关系的描述

路径：顶点 $v_p$ 到顶点 $v_q$ 之间的一条路径是指顶点序列，$v_p, v_{i_1}, v_{i_2}, \ldots, v_{i_m}, v_q$ 。
回路：第一个顶点和最后一个顶点相同的路径称为回路或环。$v_p, v_{i_1}, v_{i_2}, \ldots, v_{i_m}, v_p$ 。
简单路径：在路径序列中，顶点不重复出现的路径称为简单路径。
简单回路：除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路。
路径长度：路径上边的数目。
点到点的距离：从顶点 $u$ 出发到顶点 $v$ 的最短路径（若存在），此路径的长度称为从 $u$ 到 $v$ 的距离。若从 $u$ 到 $v$ 根本不存在路径，则记该距离为无穷（$\infty$）。

若一个图有n个顶点，且边数大于n-1，则此图一定有环。

在有向图中，如果从顶点v到顶点w和从顶点w到顶点v都有路径，则称这两个顶点是强连通的。
在无向图中，如果从顶点v到顶点w有路径存在，则称这两个顶点是连通的。

图的连通性（连通图、强连通图）

连通图：若图G中任意两个顶点都是连通的，则称图G为连通图，否则称为非连通图。

对于有 $n$ 个顶点的无向图 $G$，若 $G$ 是连通图，则最少有 $n-1$ 条边。若 $G$ 是非连通图，则最多可能有$C_{n-1}^2$条边。

强连通图：若图中任何一对顶点都是强连通的，则称此图为强连通图。

对于有 $n$ 个顶点的有向图 $G$，若 $G$ 是强连通图，则最少有$n$条边（形成回路）。

连通分量：无向图中的极大连通子图（[[#子图]]必须连通，且包含尽可能多的顶点和边）称为连通分量。

说句题外的例子：如果我们把刚刚拓展到全国铁路网看作是一张图G，那么相应的京港高速铁路昌九段就是一个子图，那么相应的，大陆地区/台湾地区/海南省的铁路网就是这张图的连通分量。

强连通分量：有向图 $G$ 中的极大强连通子图（[[#子图]]必须强连通，且包含尽可能多的顶点和边）称为强连通分量。

子图

子图：设有两个图 $G = (V, E)$ 和 $G' = (V', E')$，若 $V' \subseteq V$ 且 $E' \subseteq E$，则称 $G'$ 是 $G$ 的子图。若 $V(G') = V(G)$，则称 $G'$ 为 $G$ 的生成子图（即包含全部顶点的子图）。

生成树&生成森林

连通图的生成树是包含全部顶点的极小连通子图（边要尽可能地少，但要保持连通）。若顶点为n，则有n-1条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。
在非连通图中，连通分量的生成树构成非连通图的生成森林。

边的权、带权图

边的权：在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。
带权图（网）：边上带有权值的图称为带权图，也称网。
带权路径长度：当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度。 ^Cite1

还是上面的例子，如果我们在每个边上表明两个车站之间的距离，那么这个图就是带权图。

几种特殊的图

无向完全图：无向图中任意两个顶点之间都存在边。

若无向图的顶点数 $|V| = n$，则边的数目 $|E|$ 的取值范围为 $0 \leq |E| \leq \frac{n(n-1)}{2}$ 。（即$C_n^2$）

有向完全图：有向图中任意两个顶点之间都存在方向相反的两条弧。

若有向图的顶点数$|V|=n$，则弧的数目 $|E|$ 的取值范围为 $0 \leq |E| \leq n(n-1)$ 。（即$2C_n^2$）

稀疏图：边数很少的图。反之称为稠密图。

注意，以上没有一个绝对的界限，一般来说$|E| < |V|log|V|$时，可以将G视为稀疏图

有向树：一个顶点的入度为0、其余顶点的入度为1的有向图，称为有向树。

树，不存在回路且连通的无向图，n个顶点的树有n-1条边。

图的存储

邻接矩阵法

定义

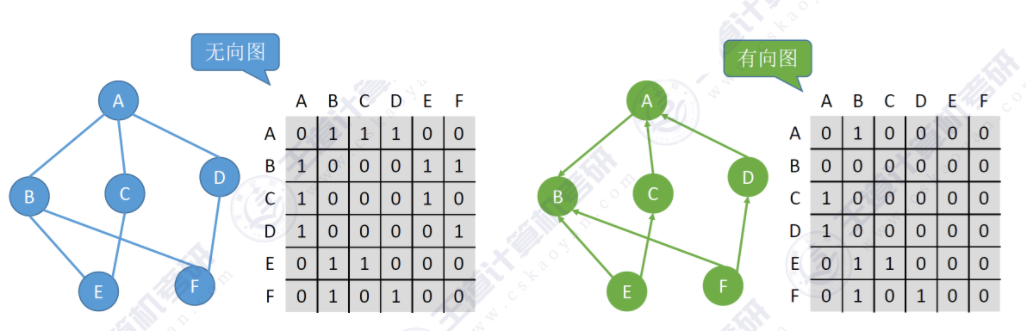
邻接矩阵是指用一个一维数组存储图中顶点的信息，用一个二维数组存储图中边的信息（各顶点间的邻接关系），存储顶点之间邻接关系的二维数组称为邻接矩阵。

结点数为$n$的图$G = (V, E)$的邻接矩阵A是$n*n$的。将G的顶点编号为$v_1, v_2, \ldots, v_n$，则：

$$ A[i][j] = \begin{cases} 1, & \text{若}(v_i, v_j)\text{或}<v_i,v_j>\text{是E(G)中的边} \\ 0, & \text{若}(v_i, v_j)\text{或}<v_i,v_j>\text{不是E(G)中的边} \end{cases} $$

以下是图的邻接矩阵示意图：

图的邻接矩阵示例

以下是带权图（网的）的邻接矩阵示意图：

带权图的邻接矩阵示例

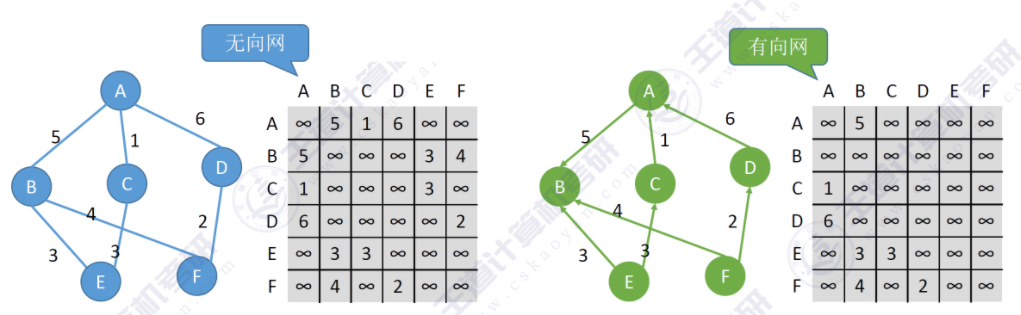
对角线元素也经常用0表示

代码实现

//图的邻接矩阵
#define MaxVertexNum 100 // 顶点数目的最大值
typedef struct{
  char Vex[MaxVertexNum];//顶点表(这里可以拓展，存更多的信息)
  int Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵(当然也可以是bool型)
  int vexnum,edgenum;//顶点数和边数
}MGraph;

//带权图的邻接矩阵（同时也对其进行了一定的拓展）
#define MaxVertexNum 100 // 顶点数目的最大值
#define INFINITY MAX_INT //无穷大
typedef char VertexType;//顶点类型
tyepedef int EdgeType;//边的权值类型
typedef struct{
  VertexType Vex[MaxVertexNum];//顶点表(这里可以拓展，存更多的信息)
  EdgeType Edge[MaxVertexNum][MaxVertexNum];//这里需要存储边的权值
  int vexnum,edgenum;//顶点数和边数
}MGraph;

特点

对无向图，第i个结点的度$TD(i)$=第i行（或第i列）非零元素的个数
对有向图，第i个结点的入度$ID(i)$=第i行非零元素（或非∞元素）的个数
对有向图，第i个结点的出度$OD(i)$=第i列非零元素（或非∞元素）的个数
第i个结点的度=第i行、第i列的非零元素个数之和
对于无向图的邻接矩阵一定是一个[[数组和特殊矩阵#对称矩阵]]，所以在实际存储邻接矩阵的时候只需要存储上（或下）三角矩阵的元素。
稠密图适合用此方法表示。
设图G的邻接矩阵为A（矩阵元素为0/1），则$A^n$的元素$A^n[i][j]$等于由顶点i到顶点j的长度为n的路径的数目。

复杂度分析

空间复杂度：$O(|V|^2)$ ，其只和顶点数相关，和实际的边数无关
邻接矩阵法求顶点的度/出度/入度的时间复杂度：$O(|V|)$
适合用于存储稠密图
无向图的邻接矩阵是对称矩阵，可以压缩存储（只存储上三角区/下三角区）

邻接表法

定义

邻接表，对图G中的每个顶点$v_i$建立一个单链表，第i个单链表中的结点表示依附于顶点$v_i$的边（对于有向图而言则是以顶点$v_i$为尾的弧，假设1->2，则挂在1上），这个单链表就是顶点$v_i$的边表（有向图中叫做出边表）。边表的头指针和顶点的数据信息采用顺序存储，称为顶点表，所以在邻接表中存在两种结点，顶点表结点和边表结点。

如下图所示，即为顶点表和边表的结点结构

顶点表和边表的数据结构

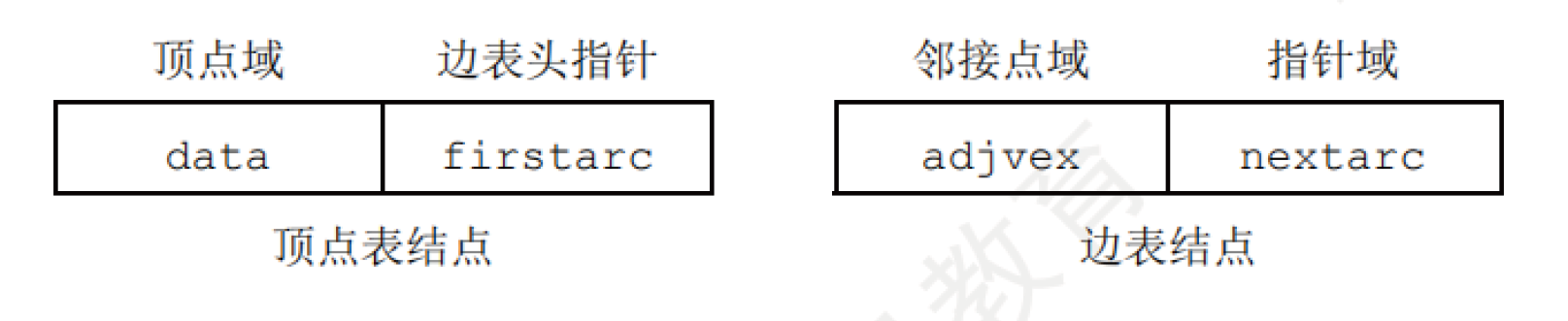
顶点表结点由顶点信息（存储顶点相关信息）和边表头指针（指向第一条边的边表结点）组成，边表结点由邻接点域（存储头结点顶点邻接的顶点编号）和指针域（指向下一条的边表结点）组成。

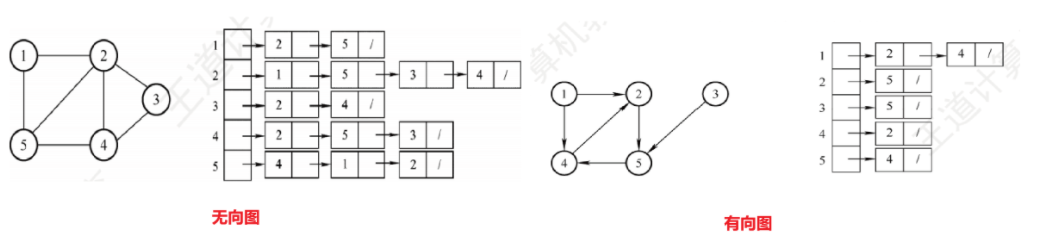
如图所示是有向图和无向图邻接表表示法的示例：

有向图和无向图邻接表表示法示例

代码实现

#define MaxVertexNum 100 // 最大顶点数
typedef struct ArcNode{ //边表结点
    int adjvex;         // 该弧指向的顶点的位置
    struct ArcNode *next; // 指向下一条边的指针
    // 其他信息（如权值等）可以在此处添加
} ArcNode;
typedef struct VNode{ //顶点表结点
    VertexType data; // 顶点信息
    ArcNode *first; // 指向第一条弧的指针
} VNode,AdjList[MaxVertexNum];
typedef struct{
    AdjList vertices; //邻接表
    int vexnum,arcnum; //顶点数和弧数
} ALGraph;

特点

适用于稀疏图
表示不唯一

复杂度分析

空间复杂度：$O(|V| + |E|)$（有向图），$O(|V| + 2|E|)$（无向图），其和顶点数、边数相关。
对于稀疏图，邻接表法比邻接矩阵法更节省空间。

十字链表法

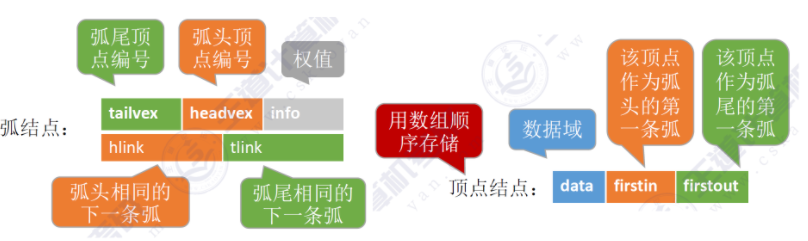
十字链表是有向图的一种存储结构，十字链表中，每个弧有个结点，每个顶点也有一个结点。

下面是一个弧节点和顶点结点的示意图：

弧节点和顶点结点的示意图

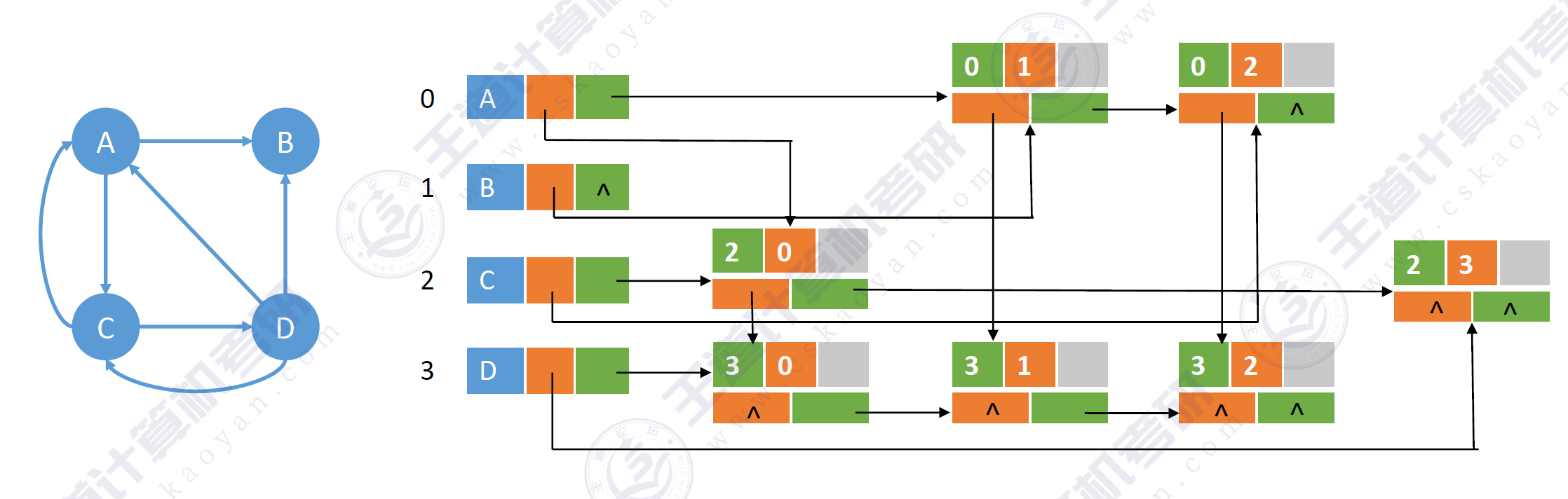
以下是一个十字链表存储有向图的示意图：

十字链表存储有向图的示意图

空间复杂度：$O(|V| + |E|)$
沿着绿色线路则是出边
沿着橙色线路则是入边
只能存储有向图
十字链表表示是不唯一的，但是一个十字链表表示唯一确定的一个图。

邻接多重表

邻接多重表是无向图的一种链式存储结构。与十字链表类似的是其边也用一个结点表示，

下面是一个邻接多重表的边节点和顶点结点的示意图：

邻接多重表的边节点和顶点结点的示意图

以下是一个邻接多重表存储无向图的示意图：

邻接多重表存储无向图的示意图

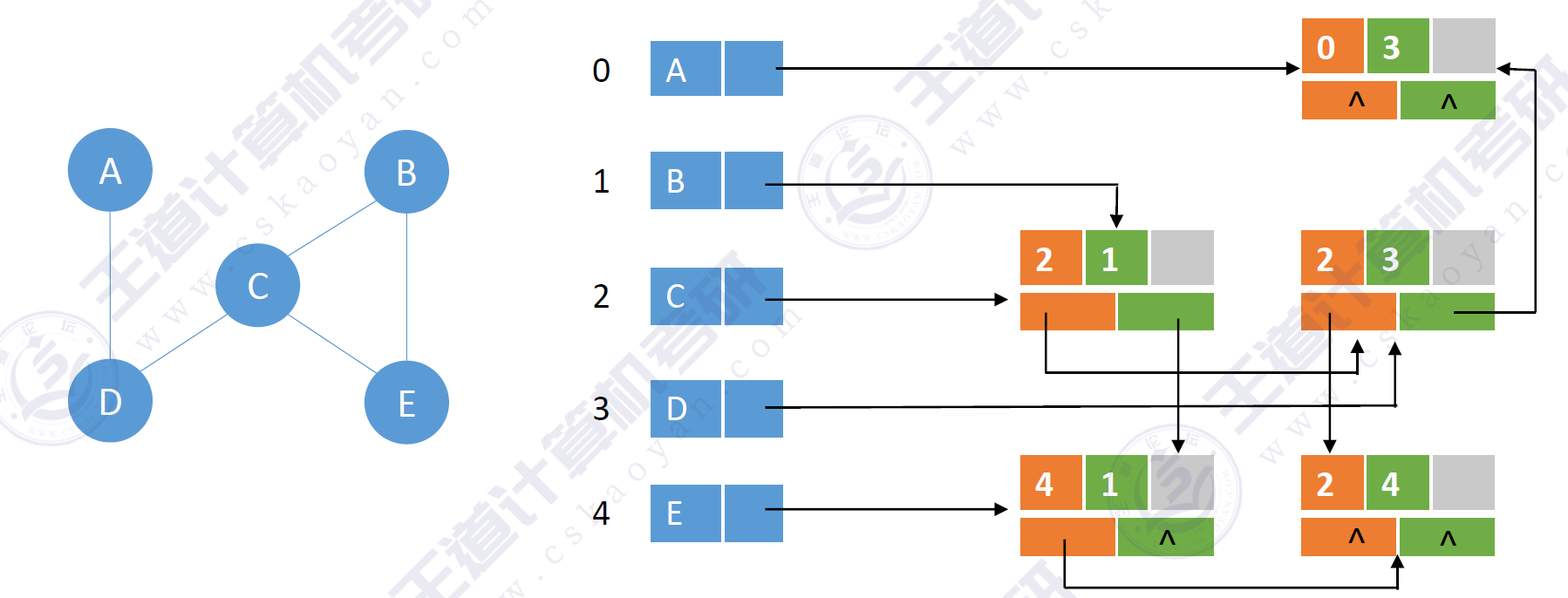
空间复杂度：$O(|V| + |E|)$
只存储无向图

图的存储四种方法对比

属性	邻接矩阵	邻接表	十字链表	邻接多重表
空间复杂度	$O(\vert V\vert^2)$	无向图 $O(\vert V\vert + 2\vert E\vert)$，有向图 $O(\vert V\vert + \vert E\vert)$	$O(\vert V\vert + \vert E\vert)$	$O(\vert V\vert + \vert E\vert)$
找相邻边	遍历对应行或列时间复杂度为$O(\vert V\vert)$	找有向图的入边必须遍历整个邻接表	很方便	很方便
删除边或顶点	删除边很方便，删除顶点需要大量移动数据	无向图中删除边或顶点都不方便	很方便	很方便
适用于	稠密图	稀疏图和其他	只能存有向图	只能存无向图
表示方式	唯一	不唯一	不唯一	不唯一

图的基本操作

Adjacent(G, x, y)
判断图 $G$ 是否存在边 $\langle x, y \rangle$ 或 $(x, y)$。
Neighbors(G, x)
列出图 $G$ 中与结点 $x$ 邻接的所有顶点。
InsertVertex(G, x)
在图 $G$ 中插入顶点 $x$。
DeleteVertex(G, x)
从图 $G$ 中删除顶点 $x$ 及其相关的所有边。
AddEdge(G, x, y)
若无向边 $(x, y)$ 或有向边 $\langle x, y \rangle$ 不存在，则向图 $G$ 中添加该边。
RemoveEdge(G, x, y)
若无向边 $(x, y)$ 或有向边 $\langle x, y \rangle$ 存在，则从图 $G$ 中删除该边。
FirstNeighbor(G, x)
求图 $G$ 中顶点 $x$ 的第一个邻接点，若有则返回顶点号；若 $x$ 没有邻接点或图中不存在 $x$，则返回 $-1$。
NextNeighbor(G, x, y)
假设图 $G$ 中顶点 $y$ 是顶点 $x$ 的一个邻接点，返回除 $y$ 之外顶点 $x$ 的下一个邻接点的顶点号；若 $y$ 是 $x$ 的最后一个邻接点，则返回 $-1$。
Get_edge_value(G, x, y)
获取图 $G$ 中边 $(x, y)$ 或 $\langle x, y \rangle$ 对应的权值。
Set_edge_value(G, x, y, v)
设置图 $G$ 中边 $(x, y)$ 或 $\langle x, y \rangle$ 的权值为 $v$。
除此之外，还有[[#图的遍历|图的遍历]]相关操作。

图的遍历

广度优先搜索

广度优先搜索（BFS，Breadth-First Search）会优先考虑最早被发现的顶点，也就是说离起点越近的顶点其优先级越高。

基本思想

类似于二叉树的层序遍历。基本思想是：首先访问起始顶点v，接着由v出发，依次访问v的各个未访问过的邻接顶点$w_1,w_2,...,w_i$,然后依次访问$w_1,w_2,...,w_i$的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点……。

为了实现逐层访问，必须借助一个辅助队列，用来记忆正在访问的顶点的下一层顶点。

代码实现

bool Visited[MAX_VERTEX_NUM]; // 访问标记数组
void BFSTraverse(Graph G) {
  for(int i = 0; i < G.vexnum; i++){
    Visited[i] = false; // 初始化访问标记数组
  }
  InitQueue(Q);
  for(int i = 0; i < G.vexnum; i++){//这里为了保证此图如果是一个非连通图，也能达成目的
    if(!Visited[i]){
      BFS(G, i);
    }
  }
}
//用邻接表实现的广度优先搜索算法
void BFS(ALGraph G, int i) {
  visit(i);//对i号结点访问
  Visited[i] = true; // 标记i号结点已访问
  EnQueue(Q, i); // 将i号结点入队
  while(!QueueEmpty(Q)) {
    DeQueue(Q, v); // 队头结点出队
    for(p=G.vertices[v].first; p!=NULL;p=p->next){// 遍历v的边表
      w=p->adjvex; // 获取邻接点
      if(!Visited[w]){ // 如果邻接点未访问
        visit(w); // 访问邻接点
        Visited[w] = true; // 标记邻接点已访问
        EnQueue(Q, w); // 将邻接点入队
      }
    }
  }
}
//使用邻接矩阵实现的广度优先搜索算法
void BFS(MGraph G, int i) {
  visit(i); // 对i号结点访问
  Visited[i] = true; // 标记i号结点已访问
  EnQueue(Q, i); // 将i号结点入队
  while(!QueueEmpty(Q)) {
    DeQueue(Q, v); // 队头结点出队
    for(int j = 0; j < G.vexnum; j++) { // 遍历v的邻接矩阵
      if(G.Edge[v][j] && !Visited[j]) { // 如果存在边且邻接点未访问
        visit(j); // 访问邻接点
        Visited[j] = true; // 标记邻接点已访问
        EnQueue(Q, j); // 将邻接点入队
      }
    }
  }
}

对于⽆向图，调⽤BFS函数的次数=连通分量数

复杂度分析

空间复杂度：最坏情况，辅助队列⼤⼩为 $O(|V|)$
时间复杂度: 邻接矩阵需要访问V个顶点，V个顶点又要访问V个顶点，所以时间复杂度为 $O(|V|^2)$，邻接表访问V个顶点，每个顶点访问其边表，边表的总长度为$|E|$，所以时间复杂度为 $O(|V| + |E|)$。

BFS算法求解单源最短路径问题

如果是一个不带权的图，广度优先搜索可以用来求解单源最短路径问题。广度优先搜索的每次访问都是从当前顶点到其邻接顶点的距离为1，因为广度优先搜索总是按照距离由近至远来遍历图中每个顶点的。具体代码示例如下：

void BFS_ShortestPath(MGraph G, int u) {
  //d[i]表示从u到i的最短距离
  for(int i = 0; i < G.vexnum; i++) {
    d[i] = INFINITY; // 初始化距离为无穷大
    Visited[i] = false; // 初始化访问标记
    path[i] = -1;//这里引入一个path数组，记录从起点到i的路径
  }
  d[u] = 0; // 起点到自身的距离为0
  EnQueue(Q, u); // 将起点入队
  Visited[u] = true; // 标记起点已访问
  while(!QueueEmpty(Q)) {
    DeQueue(Q, v); // 队头结点出队
    for(w=FirstNeighbor(G,v); w!=-1; w=NextNeighbor(G,v,w)) {
      if(!Visited[w]) { // 如果邻接点未访问
        Visited[w] = true; // 标记邻接点已访问
        d[w] = d[v] + 1; // 更新距离
        path[w] = v; // 记录路径
        EnQueue(Q, w); // 将邻接点入队
      }
    }
  }
}

广度优先生成树

在广度遍历的过程中，广度优先遍历的过程中，生成的树就是广度优先生成树。⼴度优先⽣成树由⼴度优先遍历过程确定。由于一定的图邻接矩阵表示法是唯一的，其广度优先生成树也是唯一的，但由于邻接表存储一个图不是唯一的，故其广度优先生成树也不是唯一的。

对⾮连通图的⼴度优先遍历，可得到⼴度优先⽣成森林

深度优先搜索

深度优先搜索（DFS，Depth-First Search）会优先考虑最后被发现的顶点，也就是说离起点越远的顶点其优先级越高。

对于同一个图，基于邻接矩阵的遍历所得到的DFS序列和BFS序列是唯一的。基于邻接表的遍历所得到的DFS序列和BFS序列不是唯一的。

基本思想

类似于树的先序遍历。首先访问图中某一起始顶点v，然后由v出发，访问于v邻接且未被访问的任一顶点$w_1$,再访问与$w_1$邻接且未被访问的任一顶点$w_2$，重复上述过程。

代码实现

bool Visited[MAX_VERTEX_NUM]; // 访问标记数组
void DFSTraverse(Graph G) {
  for(int i = 0; i < G.vexnum; i++){
    Visited[i] = false; // 初始化访问标记数组
  }
  for(int i = 0; i < G.vexnum; i++){ //这里为了保证此图如果是一个非连通图，也能达成目的
    if(!Visited[i]){
      DFS(G, i);
    }
  }
}
//用邻接表实现的深度优先搜索算法
void DFS(ALGraph G, int i) {
  visit(i); // 对i号结点访问
  Visited[i] = true; // 标记i号结点已访问
  for(p=G.vertices[i].first; p!=NULL; p=p->next) { // 遍历i的边表
    w=p->adjvex; // 获取邻接点
    if(!Visited[w]) { // 如果邻接点未访问
      DFS(G, w); // 递归访问邻接点
    }
  }
}
//使用邻接矩阵实现的深度优先搜索算法
void DFS(MGraph G, int i) {
  visit(i); // 对i号结点访问
  Visited[i] = true; // 标记i号结点已访问
  for(int j = 0; j < G.vexnum; j++) { // 遍历i的邻接矩阵
    if(G.Edge[i][j] && !Visited[j]) { // 如果存在边且邻接点未访问
      DFS(G, j); // 递归访问邻接点
    }
  }
}

复杂度分析

DFS是一个递归算法，需要一个递归工作栈，故空间复杂度$O(|V|)$

时间复杂度和BFS类似，邻接矩阵$O(|V|^2)$，邻接表$O(|V| + |E|)$。

深度优先生成树

深度优先搜索也会产生一颗深度优先生成树，和BFS类似。

对⾮连通图的深度优先遍历，可得到深度优先生成森林。

图的遍历与图的连通性

对于无向图，调用BFS和DFS的次数等于它的连通分量数量。

有向图，非强连通分量调用一次BFS或DFS无法访问到该连通分量的所有顶点。

图的应用

最小生成树

连通图的生成树是包含图中全部顶点的一个极小连通子图。若生成树的边的权值之和最小，则称为最小生成树。

官方定义：对于⼀个带权连通⽆向图G = (V, E)，⽣成树不同，每棵树的权（即树中所有边上的权值之和）也可能不同。设R为G的所有⽣成树的集合，若T为R中边的权值之和最⼩的⽣成树，则T称为G的最⼩⽣成树（Minimum-Spanning-Tree, MST）。

其性质如下：

不是唯一的.当图G中的各边权值不等时,是唯一的.
最小生成树的边的权值之和总是唯一的.而且是最小的
边数=顶点数-1
只有连通图才有⽣成树，⾮连通图只有⽣成森林
如果⼀个连通图本身就是⼀棵树，则其最⼩⽣成树就是它本身

也有两种方法求解最小生成树，分别是Prim算法和Kruskal算法。

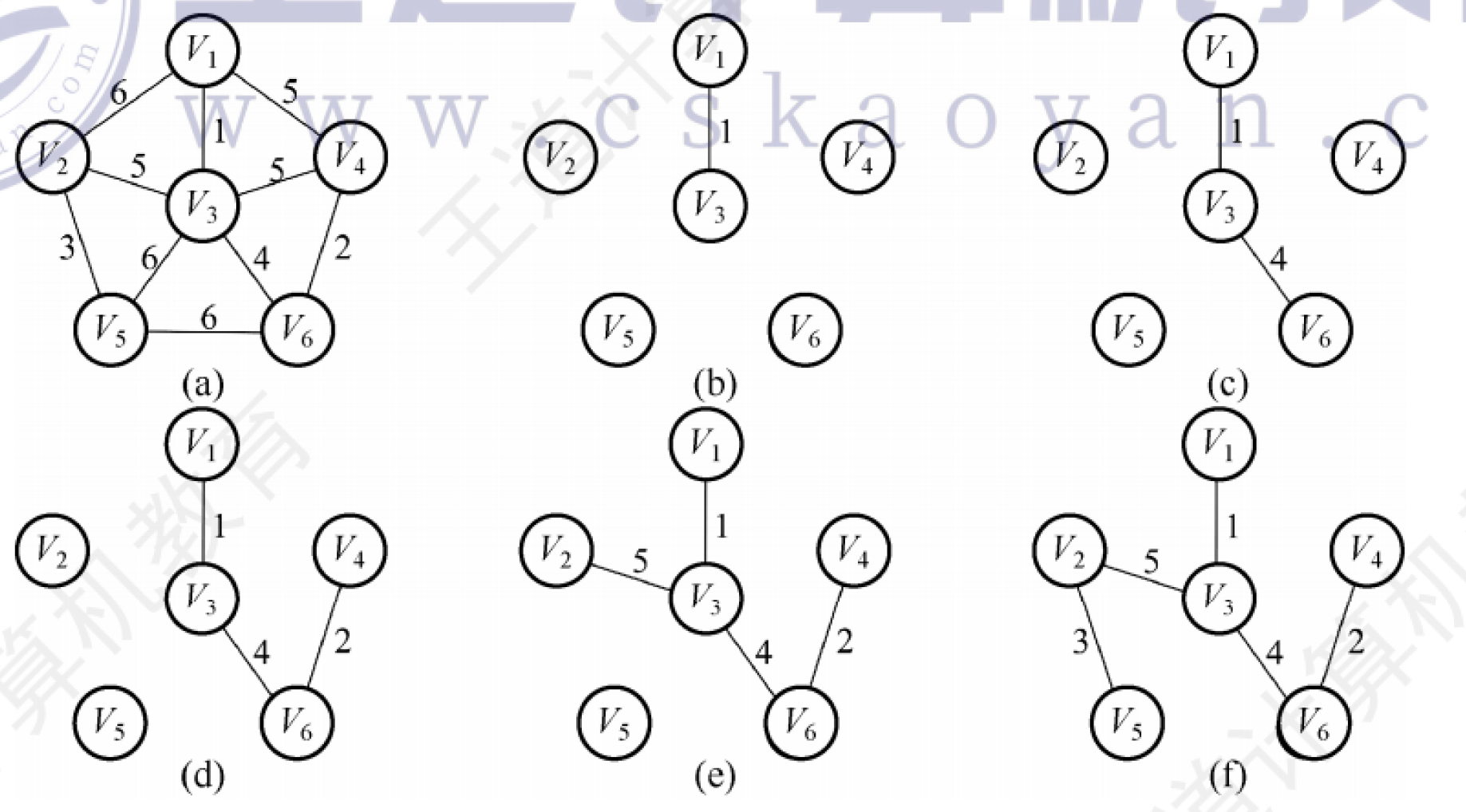
Prim算法

从某⼀个顶点开始构建⽣成树；每次将代价最⼩的新顶点纳⼊⽣成树，直到所有顶点都纳⼊为⽌。

算法步骤如图所示：

Prim算法示意图

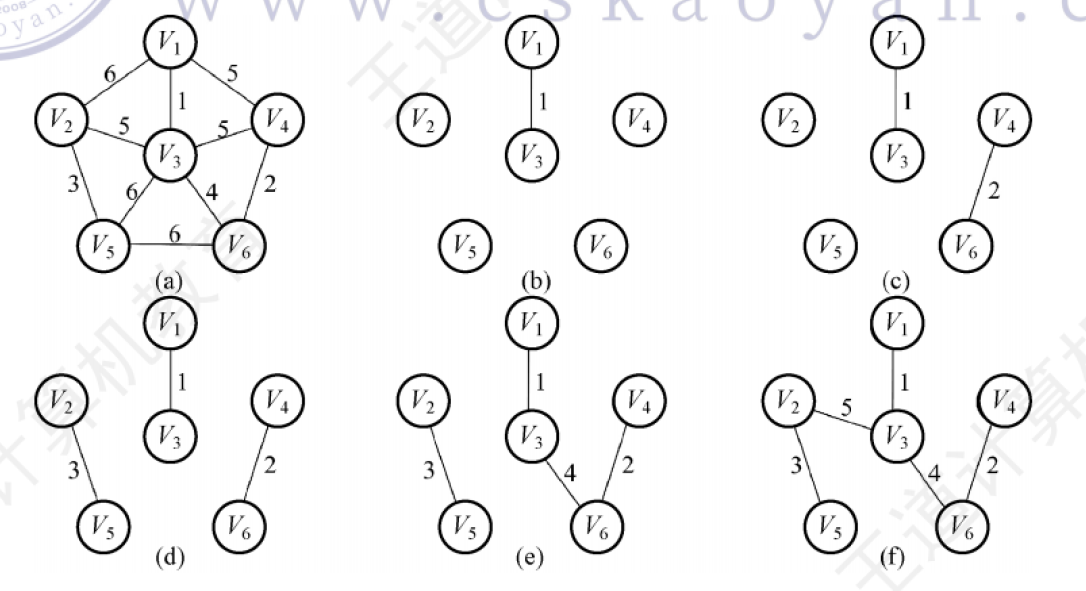
Kruskal算法

每次选择⼀条权值最⼩的边，使这条边的两头连通（原本已经连通的就不选）直到所有结点都连通。

算法步骤如图所示：

Kruskal算法示意图

Prim算法和Kruskal算法的对比

属性	Prim算法	Kruskal算法
基本思想	从某一顶点开始，逐步扩展生成树	从边的集合开始，逐步选择边加入生成树
适用场景	稠密图	稀疏图
时间复杂度	$O(\vert V \vert^2)$	$O(\vert E \vert \log \vert E \vert)$

Kruskal算法通常用堆来存储边的集合。

最短路径问题

BFS求解单源最短路径问题

详见：[[#BFS算法求解单源最短路径问题]]

Dijkstra算法单源最短路径算法

[[#^Cite1|带权路径长度]]：当图是带权图时，⼀条路径上所有边的权值之和，称为该路径的带权路径⻓度。

BFS算法适用于不带权图（或等权图）的单源最短路径问题，而Dijkstra算法适用于带权图的单源最短路径问题。

Dijkstra算法:三个辅助数组:dist[],记录由源点$v_0$到各顶点当前的最短长度;path[]表示从源点到顶点i之间的最短路径的前驱结点，final[]表示顶点i是否已经找到最短路径。

过程如下所示：

Dijkstra算法过程

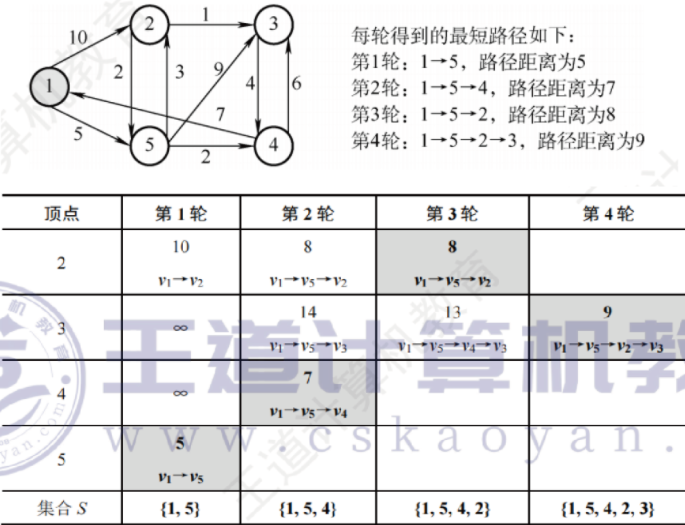
注意：Dijkstra算法不能用于带有负权边的图。

时间复杂度：$O(|V|^2)$

Floyd算法求解个各顶点间的最短路径

Floyd算法：求出每⼀对顶点之间的最短路径。

对于每一对顶点 $i$ 和 $j$，以及中间顶点 $k$，有如下递推关系：若 $A^{(k-1)}[i][j] > A^{(k-1)}[i][k] + A^{(k-1)}[k][j]$，则更新 $A^{(k)}[i][j]$ 和 $path^{(k)}[i][j]$，否则保持原值。

算法执行过程如下图所示：

Floyd算法执行过程

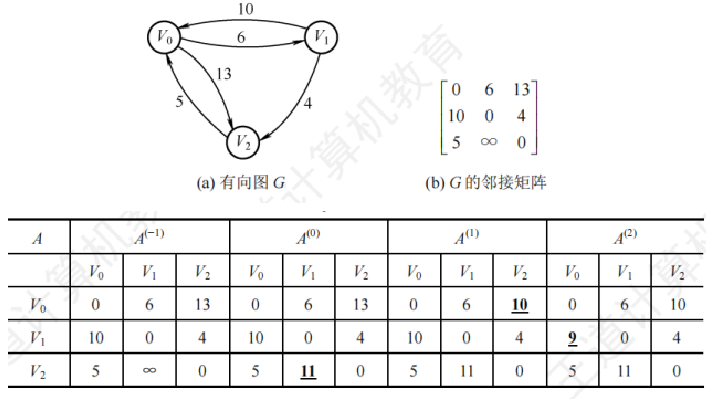
注意：Floyd可以用于负权图，Floyd 算法不能解决带有“负权回路”的图（有负权值的边组成回路），这种图有可能没有最短路径

BFS、Dijkstra和Floyd算法的对比

特性	BFS 算法	Dijkstra 算法	Floyd 算法
无权图	✓	✓	✓
带权图	✗	✓	✓
带负权值的图	✗	✗	✓
带负权回路的图	✗	✗	✗
时间复杂度	$( O(\vert V\vert^2) )$ 或 $( O(\vert V\vert + \vert E\vert) )$	$( O(\vert V\vert^2) )$	$( O(\vert V\vert^3) )$
通常用于	求无权图的单源最短路径	求带权图的单源最短路径	求带权图中各顶点间的最短路径

Dijkstra应说的话也可以求各个顶点间的最短路径，就是每个顶点执行一次Dijkstra算法，时间复杂度就是$( O(\vert V\vert^3) )$

有向无环图描述表达式

有向⽆环图：若⼀个有向图中不存在环，则称为有向⽆环图，简称DAG图（Directed Acyclic Graph）

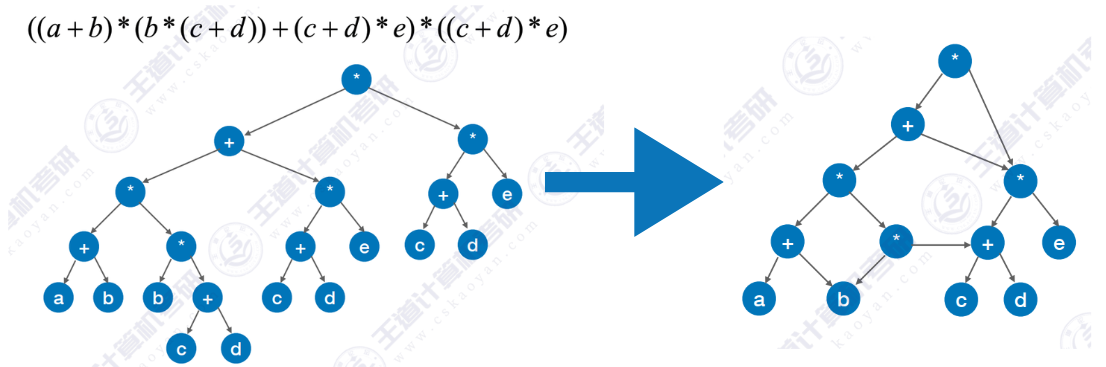
如下图是$((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e)$的二叉树表示和有向无环图表示

有向无环图描述表达式示意图

拓扑排序

AOV网（Activity On Vertex Network，顶点表示活动的网络）：用有向无环图（DAG）来表示一个工程。顶点表示活动，有向边 $\langle V_i, V_j \rangle$ 表示活动 $V_i$ 必须先于活动 $V_j$ 进行。

拓扑排序：在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序：

每个顶点出现且只出现一次。
若顶点A在序列中排在顶点B的前面，则在图中不存在从顶点B到顶点A的路径。

或定义为：拓扑排序是对有向无环图的顶点的一种排序，它使得若存在一条从顶点A到顶点B的路径，则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。

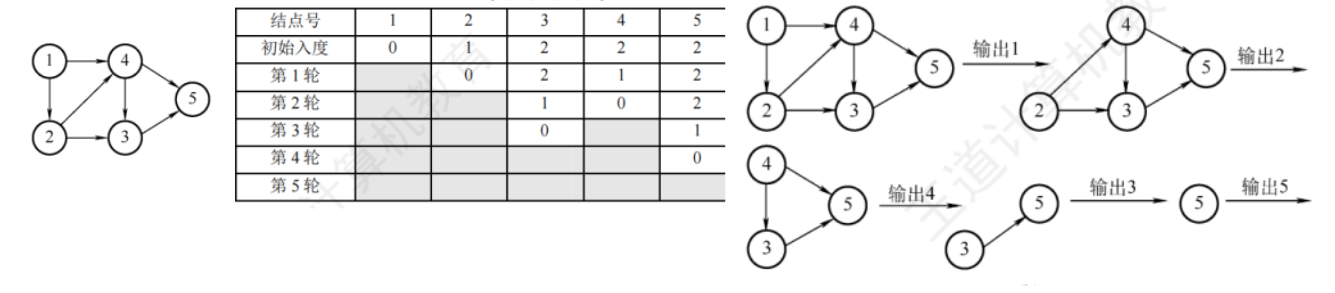
拓扑排序的算法步骤如下：

从DAG图中选择一个没有前驱的顶点并输出
从图中删除该顶点和所有以它为起点的边
重复上述过程直到当前为空或不存在无前驱的顶点(有环)为止

如下图是一个拓扑排序的例子：

拓扑排序示例

如下是基于邻接表的拓扑排序实现：

void TopologicalSort(ALGraph G) {
  InitStack(S);
  for (int i = 0; i < G.vexnum; i++) {
    if (G.vexs[i].in == 0) {// 如果顶点的入度为0
      Push(S, i); // 将顶点入栈
    }
  }
  int count = 0; // 计数器，记录已输出的顶点数
  while (!StackEmpty(S)) {
    Pop(S, v); // 栈顶元素出栈
    printf("%c ", G.vexs[v].data); // 输出顶点
    count++;// 已输出顶点数加1
    for(p=G.vexs[v].first;p!=NULL;p=p->next){
      //将所有v指向的顶点的入度减1
      w = p->adjvex; // 获取邻接点
      if(--G.vexs[w].in==0) { // 如果入度减为0
        Push(S, w); // 将入度为0的顶点入栈
      }
    }
  }
    if(count<G.vexnum) {
      printf("图中存在环，无法进行拓扑排序。\n");
    } else {
      printf("\n拓扑排序完成。\n");
    }
}

时间复杂度：$O(|V| + |E|)$（邻接表实现），$O(|V|^2)$（邻接矩阵实现）
排序结果不唯一
工程可以从入度为0的顶点开始(不存在前驱)
对于一般的图来说,其邻接矩阵是三角矩阵,则存在拓扑排序;反之不一定成立。

逆拓扑排序：拓扑排序的逆序称为逆拓扑排序。具体过程就是把出度为0的顶点输出，删除该点和以该点为终点的有向边。

关键路径

在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销（如完成活动所需的时间），称之为⽤边表示活动的⽹络，简称AOE⽹ (Activity On Edge NetWork)

AOE⽹具有以下两个性质：

只有在某顶点所代表的事件发⽣后，从该顶点出发的各有向边所代表的活动才能开始；
只有在进⼊某顶点的各有向边所代表的活动都已结束时，该顶点所代表的事件才能发⽣。另外，有些活动是可以并⾏进⾏的

在AOE⽹中仅有⼀个⼊度为0的顶点，称为开始顶点（源点），它表示整个⼯程的开始。也仅有⼀个出度为0的顶点，称为结束顶点（汇点），它表示整个⼯程的结束。

从源点到汇点的有向路径可能有多条，所有路径中，具有最⼤路径⻓度的路径称为关键路径，⽽把关键路径上的活动称为关键活动，完成整个⼯程的最短时间就是关键路径的⻓度，若关键活动不能按时完成，则整个⼯程的完成时间就会延⻓。

以下是几种参考的量的定义：

事件 $v_k$ 的最早发生时间 $v_e(k)$
指从开始顶点 $V$ 到事件 $v_k$ 的最长路径长度。计算公式为：
$$ v_e(k) = \max \{ v_e(j) + \text{Weight}(v_j, v_k) \} $$
其中 $\text{Weight}(v_j, v_k)$ 表示边 $\langle v_j, v_k \rangle$ 的权值。$v_e(k)$ 按从前往后的顺序计算。
事件 $v_k$ 的最迟发生时间 $v_l(k)$
指在不推迟整个工程完成的前提下，事件 $v_k$ 最迟必须发生的时间。计算公式为：
$$ v_l(j) = \min \{ v_l(k) - \text{Weight}(v_j, v_k) \} $$
其中 $\text{Weight}(v_j, v_k)$ 表示边 $\langle v_j, v_k \rangle$ 的权值。$v_l(j)$ 按从后往前的顺序计算。
活动 $a_i$ 的最早开始时间 $e(i)$
即该活动的起点事件的最早发生时间。若边 $\langle v_k, v_j \rangle$ 表示活动 $a_i$，则
$$ e(i) = v_e(k) $$
活动 $a_i$ 的最迟开始时间 $l(i)$
即活动终点事件的最迟发生时间减去该活动所需时间。若边 $\langle v_k, v_j \rangle$ 表示活动 $a_i$，则
$$ l(i) = v_l(j) - \text{Weight}(v_k, v_j) $$
活动 $a_i$ 的时间余量 $d(i)$
即最迟开始时间与最早开始时间之差：
$$ d(i) = l(i) - e(i) $$
$d(i)$ 表示在不增加整个工程完成时间的前提下，活动 $a_i$ 可以拖延的最大时间。若 $d(i) = 0$，则该活动为关键活动，必须如期完成。

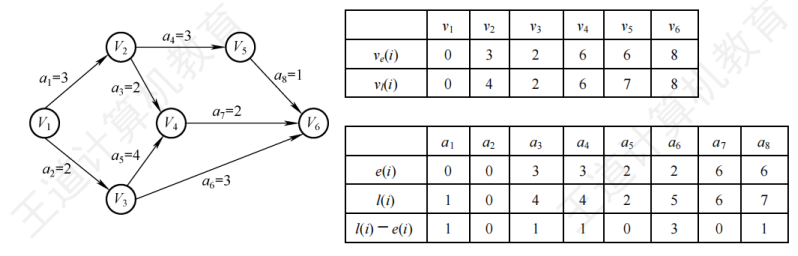
求关键路径的算法:

求所有$v_e()$
求所有$v_l()$
求所有e()
求所有l()
求所有d(),找出关键路径

d(k)=0的活动就是关键活动, 由关键活动可得关键路径

如下图所示是一个求解关键路径的示例：

求解关键路径示例

注意以下几点：

关键路径所有活动都是关键活动
关键路径不唯一
加速某一关键活动不一定缩短整个工程的工期.因为AOE网中存在多条关键路径.可能存在称为"桥"的一种特殊关键活动,它位于所有的关键路径上,只有它加速才会缩短整个工期。

番外篇：采用不同存储结构时各种图算法的时间复杂度

存储结构	Dijkstra	Floyd	Prim	Kruskal	DFS	BFS	拓扑排序	关键路径
邻接矩阵	$O(n^2)$	$O(n^3)$	$O(n^2)$	-	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(n^2)$
邻接表	-	-	-	$O(e\log _2 e)$	$O(n+e)$	$O(n+e)$	$O(n+e)$	$O(n+e)$

【计算机考研（408）- 数据结构】图

图

图的定义

有关图的相关概念

有向图和无向图

简单图和多重图

顶点的度

顶点之间的关系的描述

图的连通性（连通图、强连通图）

子图

生成树&生成森林

边的权、带权图

几种特殊的图

图的存储

邻接矩阵法

定义

代码实现

特点

复杂度分析

邻接表法

定义

代码实现

特点

复杂度分析

十字链表法

邻接多重表

图的存储四种方法对比

图的基本操作

图的遍历

广度优先搜索

基本思想

代码实现

复杂度分析

BFS算法求解单源最短路径问题

广度优先生成树

深度优先搜索

基本思想

代码实现

复杂度分析

深度优先生成树

图的遍历与图的连通性

图的应用

最小生成树

Prim算法

Kruskal算法

Prim算法和Kruskal算法的对比

最短路径问题

BFS求解单源最短路径问题

Dijkstra算法单源最短路径算法

Floyd算法求解个各顶点间的最短路径

BFS、Dijkstra和Floyd算法的对比

有向无环图描述表达式

拓扑排序

关键路径

番外篇：采用不同存储结构时各种图算法的时间复杂度