找到
8
篇与
数据结构
相关的结果
-
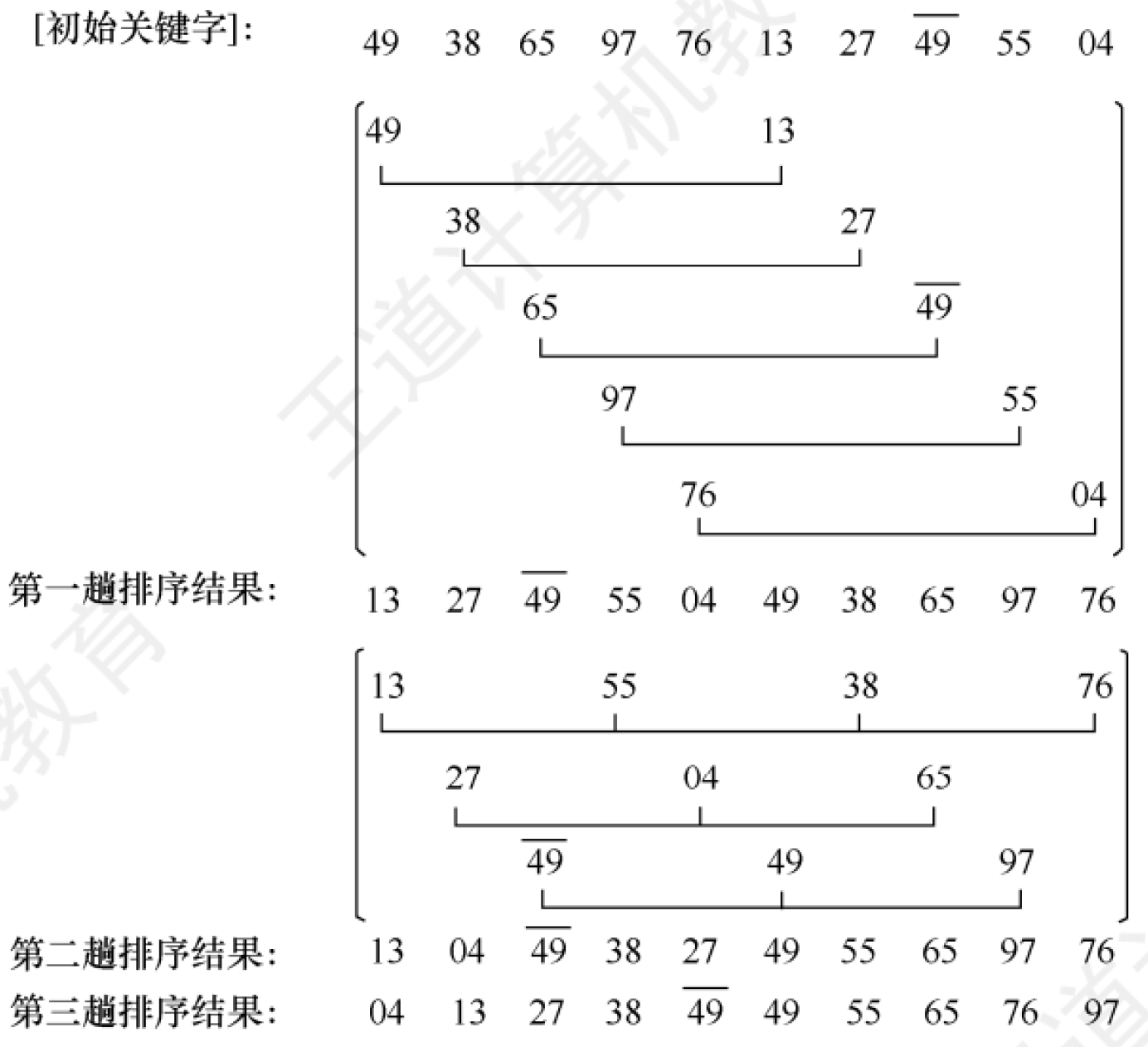
 【计算机考研(408)- 数据结构】排序 排序 排序(Sort),就是重新排列表中的元素,使表中的元素满足按关键字有序的过程。 稳定性:相同的元素,排完后相对顺序不变 内部排序:所有元素都在内存中进行排序 外部排序:元素无法都放在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动的排序 本节默认非严格递增排序。插入排序 思路 每次将⼀个待排序的记录按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成。 过程 初始 (49) 38 65 97 76 13 27 49. i=2: (38 49) 65 97 76 13 27 49. i=3: (38 49 65) 97 76 13 27 49. i=4: (38 49 65 97) 76 13 27 49. i=5: (38 49 65 76 97) 13 27 49. i=6: (13 38 49 65 76 97) 27 49. i=7: (13 27 38 49 65 76 97) 49. i=8: (13 27 38 49 49 65 76 97)这里没有体现出哨兵,就是index=0位置不存储任何东西,充当哨兵。代码 //带哨兵的直接插入排序 void InsertSort(int A[],int n){ int i,j; for(i =2;i<=n;i++){ if(A[i]<A[i-1]){ A[0] = A[i];//哨兵 for(j = i-1;A[0]<A[j];j--)//从后往前查找应该插入的地方 A[j+1] = A[j]; A[j+1] = A[0];//插入 } } } //优化版本(折半插入) void BinaryInsertSort(int A[],int n){ int i,j,low,high,mid; for(i = 2;i <= n;i++){ if(A[i] < A[i-1]){ A[0] = A[i];//哨兵 /* 先找到插入位置 */ low = 1; high = i-1; while(low <= high){ mid = (low + high) / 2; if(A[0] < A[mid]) high = mid - 1; else low = mid + 1; } /* 再执行插入 */ for(j = i-1; j >= low; j--) A[j+1] = A[j]; A[low] = A[0]; } } }复杂度分析 时间复杂度:O(n^2),最坏情况下需要进行n次插入,每次插入需要移动O(n)个元素。 空间复杂度:O(1),只使用了常数级别的额外空间。 稳定性:稳定 当 $A[mid]==A[0]$ 时,为了保证算法的“稳定性”,应继续在 mid 所指位置右边寻找插入位置希尔排序 思路 将排序表分割成$L[i,i+d,i+2d,..,i+kd]$的特殊形式。先取一个小于n的步长$d_1$,把表中的全部记录分成$d_1$组,所有距离为$d_1$的倍数的记录放在同一组中,各组中进行直接插入排序;然后取$d_2 < d_1$,最后的增量一定是1。 过程 希尔排序过程图片 代码 void ShellSort(ElemType A[],int n){ for(dk=n/2;dk>=1;dk=dk/2){//增量不是死的,也就是说这个循环会变化的 for(i=dk+1;i<=n;++i){ if(A[i]<A[i-dk]){ A[0]=A[i];//只是暂存 for(j=i-dk;j>0&&A[0]<A[j];j-=dk){ A[j+dk]=A[j]; // 后移 } A[j+dk]=A[0]; } } } }复杂度分析 空间复杂度:O(1),只使用了常数级别的额外空间。 时间复杂度:$O(n^{1.3})$,最坏情况下$O(n^2)$。 稳定性:不稳定。 冒泡排序 思路 一趟冒泡,将最小的元素交换到待排序列的第一个位置.冒泡排序中所产生的有序子序列一定是全局有序的。冒泡排序算法的结束条件时在一趟排序过程中没有发生关键字交换。 过程 冒泡排序示例图片 代码 void BubbleSort(ElemType A[],int n){ for(i=0;i<n-1;i++){ flag=false; // 本趟是否发生交换 for(j=n-1;j>i;j--){ if(A[j-1].key>A[j].key){ swap(A[j-1],A[j]); flag=true; } } if(flag==false){ return; // 没有发生交换,结束 } } }复杂度分析 时间复杂度:$O(n^2)$,最坏情况下需要进行n次插入,每次插入需要移动O(n)个元素。平均也是$O(n^2)$。 空间复杂度:O(1),只使用了常数级别的额外空间。 稳定性:稳定 快速排序 思路 每次取一个基准元素pivot。每趟排序后,pivot位置确定。 过程 确定枢轴位置的过程: 枢轴图片 快排整体过程: 整体过程图片 代码 void QuickSort(ElemType A[], int low, int high) { if (low < high) { int pivot = Partition(A, low, high); QuickSort(A, low, pivot - 1); QuickSort(A, pivot + 1, high); } } int Partition(ElemType A[], int low, int high) { ElemType pivot = A[low]; while (low < high) { while (low < high && A[high] >= pivot) high--; A[low] = A[high]; while (low < high && A[low] <= pivot) low++; A[high] = A[low]; } A[low] = pivot; return low; }复杂度分析 时间复杂度:$O(n \log _2 n)$,平均情况下,快速排序的时间复杂度为 $O(n \log_2 n)$,最坏情况下为 $O(n^2)$。 空间复杂度:$O(\log_2 n)$,主要是递归调用栈的空间。 稳定性:不稳定。 简单选择排序 思路 假设排序表为$L[1...n]$ ,第i趟排序从$L[i...n]$中选择关键字最小的元素与L(i)交换。 代码 void SelectionSort(ElemType A[], int n) { for (int i = 1; i < n; i++) { int minIndex = i; for (int j = i + 1; j <= n; j++) { if (A[j] < A[minIndex]) { minIndex = j; } } swap(A[i], A[minIndex]); } }复杂度分析 时间复杂度:$O(n^2)$,最坏情况下需要进行n次选择,每次选择需要遍历O(n)个元素。 空间复杂度:O(1),只使用了常数级别的额外空间。 稳定性:不稳定。 堆排序 思路 将待排序的数组看作一个完全二叉树,只要满足了父节点大于等于子节点,就是大根堆,反之亦然,经常用此来实现优先队列 过程 自下而上调整为大根堆: 自下往上调整为大根堆图片 之后,把根节点与最后一个节点交换,然后再对除最后一个结点以外的所有元素进行调整,直到整个堆有序。 删除: 删除图片 插入: 插入图片 代码 代码不是那么重要哈~void HeapSort(ElemType A[], int n) { BuildMaxHeap(A, n); for (int i = n - 1; i > 0; i--) { swap(A[0], A[i]); MaxHeapify(A, 0, i); } } void BuildMaxHeap(ElemType A[], int n) { for (int i = n / 2 - 1; i >= 0; i--) { MaxHeapify(A, i, n); } } void MaxHeapify(ElemType A[], int i, int n) { int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; if (left < n && A[left] > A[largest]) largest = left; if (right < n && A[right] > A[largest]) largest = right; if (largest != i) { swap(A[i], A[largest]); MaxHeapify(A, largest, n); } }复杂度分析 时间复杂度:$O(n \log_2 n)$,主要是建堆和调整堆的时间复杂度。 空间复杂度:$O(1)$,只使用了常数级别的额外空间。 稳定性:不稳定。 归并排序 思路 二路归并:将待排序序列分为两部分,分别对这两部分进行归并排序,然后将已排序的两部分合并成一个整体有序序列。 过程 二路归并图片 代码 void MergeSort(ElemType A[], int left, int right) { if (left < right) { int mid = (left + right) / 2; MergeSort(A, left, mid); MergeSort(A, mid + 1, right); Merge(A, left, mid, right); } } void Merge(ElemType A[], int left, int mid, int right) { int i = left, j = mid + 1, k = 0; ElemType* temp = new ElemType[right - left + 1]; while (i <= mid && j <= right) { if (A[i] < A[j]) { temp[k++] = A[i++]; } else { temp[k++] = A[j++]; } } while (i <= mid) temp[k++] = A[i++]; while (j <= right) temp[k++] = A[j++]; for (i = left, k = 0; i <= right; i++, k++) { A[i] = temp[k]; } delete[] temp; }复杂度分析 时间复杂度:$O(n \log_2 n)$,主要是分割和合并的时间复杂度。 空间复杂度:$O(n)$,需要额外的空间来存放合并后的结果。 稳定性:稳定。 基数排序 思路 基数排序并不基于比较和移动进行排序,而是基于关键字的值进行排序,将所有数据收集到一个数组中,然后根据关键字的某一位进行排序,直到所有的关键字都排序完成。 为实现多关键字排序,通常有两种方法:第一种是最高位优先(MSD)法,按关键字位权重递减依次逐层划分成若干更小的子序列,最后将所有子序列依次连接成一个有序序列;第二种是最低位优先(LSD)法,按关键字位权重递增依次进行排序,最后形成一个有序序列。。 过程 通常采用链式基数排序,假设对如下10个记录进行排序:278 109 063 930 589 184 505 269 008 083 这个时候基数r=10,把每一个整数分为个位,十位,百位三个子关键字,进行三趟分配和收集,如下图所示: 基础排序过程图片 复杂度分析 空间复杂度:r个队列(r个队头指针,r个队尾指针),故为$O(r)$ 时间复杂度:d趟,每趟都要遍历整个数组,还要合并r个队列,故为$O(d(n+r))$ 稳定性:稳定 适用:顺序存储和链式存储的线性表。 计数排序 不在大纲内,但是思想很重要!思路 计数排序的基本思想是:对于待排序的数组,首先找出其中的最大值和最小值,然后统计每个元素出现的次数,最后根据统计结果将元素放回原数组中。 过程 找到待排序数组的最大值和最小值。 创建一个计数数组,大小为最大值与最小值之差加一,用于统计每个元素出现的次数。 遍历待排序数组,将每个元素的出现次数存入计数数组中。 根据计数数组的统计结果,将元素放回原数组中。 代码 void CountingSort(ElemType A[], int n) { if (n <= 0) return; // 找到最大值和最小值 ElemType maxVal = A[0]; ElemType minVal = A[0]; for (int i = 1; i < n; i++) { if (A[i] > maxVal) maxVal = A[i]; if (A[i] < minVal) minVal = A[i]; } // 创建计数数组 int range = maxVal - minVal + 1; int* count = new int[range](); for (int i = 0; i < n; i++) { count[A[i] - minVal]++; } // 将元素放回原数组 int index = 0; for (int i = 0; i < range; i++) { while (count[i] > 0) { A[index++] = i + minVal; count[i]--; } } delete[] count; }复杂度分析 时间复杂度:$O(n + k)$,其中 n 是待排序数组的长度,k 是计数数组的长度。 空间复杂度:$O(k)$,需要额外的空间来存放计数数组。 稳定性:稳定。 内部排序算法性能分析 算法种类最好情况平均情况最坏情况空间复杂度是否稳定每次能否固定一个位置比较次数与初始状态有关直接插入排序$O(n)$$O(n^2)$$O(n^2)$O(1)是否是冒泡排序$O(n)$$O(n^2)$$O(n^2)$O(1)是是是简单选择排序$O(n^2)$$O(n^2)$$O(n^2)$O(1)否是否希尔排序 O(1)否否是快速排序$O(nlog_2n)$$O(nlog_2n)$$O(n^2)$$O(log_2n)$否是是堆排序$O(nlog_2n)$$O(nlog_2n)$$O(nlog_2n)$$O(1)$否是是2路归并排序$O(nlog_2n)$$O(nlog_2n)$$O(nlog_2n)$$O(n)$是否-基数排序$O(d(n+2))$$O(d(n+r))$$O(d(n+r))$$O(r)$是否-外部排序 外部排序暂时不整理在一般情况下,对于 k–路平衡归并来说,若 (m-1)%(k-1)=0,则不需要增加虚段;否则需附加 k-(m-1)%(k-1)-1 个虚段。
【计算机考研(408)- 数据结构】排序 排序 排序(Sort),就是重新排列表中的元素,使表中的元素满足按关键字有序的过程。 稳定性:相同的元素,排完后相对顺序不变 内部排序:所有元素都在内存中进行排序 外部排序:元素无法都放在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动的排序 本节默认非严格递增排序。插入排序 思路 每次将⼀个待排序的记录按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成。 过程 初始 (49) 38 65 97 76 13 27 49. i=2: (38 49) 65 97 76 13 27 49. i=3: (38 49 65) 97 76 13 27 49. i=4: (38 49 65 97) 76 13 27 49. i=5: (38 49 65 76 97) 13 27 49. i=6: (13 38 49 65 76 97) 27 49. i=7: (13 27 38 49 65 76 97) 49. i=8: (13 27 38 49 49 65 76 97)这里没有体现出哨兵,就是index=0位置不存储任何东西,充当哨兵。代码 //带哨兵的直接插入排序 void InsertSort(int A[],int n){ int i,j; for(i =2;i<=n;i++){ if(A[i]<A[i-1]){ A[0] = A[i];//哨兵 for(j = i-1;A[0]<A[j];j--)//从后往前查找应该插入的地方 A[j+1] = A[j]; A[j+1] = A[0];//插入 } } } //优化版本(折半插入) void BinaryInsertSort(int A[],int n){ int i,j,low,high,mid; for(i = 2;i <= n;i++){ if(A[i] < A[i-1]){ A[0] = A[i];//哨兵 /* 先找到插入位置 */ low = 1; high = i-1; while(low <= high){ mid = (low + high) / 2; if(A[0] < A[mid]) high = mid - 1; else low = mid + 1; } /* 再执行插入 */ for(j = i-1; j >= low; j--) A[j+1] = A[j]; A[low] = A[0]; } } }复杂度分析 时间复杂度:O(n^2),最坏情况下需要进行n次插入,每次插入需要移动O(n)个元素。 空间复杂度:O(1),只使用了常数级别的额外空间。 稳定性:稳定 当 $A[mid]==A[0]$ 时,为了保证算法的“稳定性”,应继续在 mid 所指位置右边寻找插入位置希尔排序 思路 将排序表分割成$L[i,i+d,i+2d,..,i+kd]$的特殊形式。先取一个小于n的步长$d_1$,把表中的全部记录分成$d_1$组,所有距离为$d_1$的倍数的记录放在同一组中,各组中进行直接插入排序;然后取$d_2 < d_1$,最后的增量一定是1。 过程 希尔排序过程图片 代码 void ShellSort(ElemType A[],int n){ for(dk=n/2;dk>=1;dk=dk/2){//增量不是死的,也就是说这个循环会变化的 for(i=dk+1;i<=n;++i){ if(A[i]<A[i-dk]){ A[0]=A[i];//只是暂存 for(j=i-dk;j>0&&A[0]<A[j];j-=dk){ A[j+dk]=A[j]; // 后移 } A[j+dk]=A[0]; } } } }复杂度分析 空间复杂度:O(1),只使用了常数级别的额外空间。 时间复杂度:$O(n^{1.3})$,最坏情况下$O(n^2)$。 稳定性:不稳定。 冒泡排序 思路 一趟冒泡,将最小的元素交换到待排序列的第一个位置.冒泡排序中所产生的有序子序列一定是全局有序的。冒泡排序算法的结束条件时在一趟排序过程中没有发生关键字交换。 过程 冒泡排序示例图片 代码 void BubbleSort(ElemType A[],int n){ for(i=0;i<n-1;i++){ flag=false; // 本趟是否发生交换 for(j=n-1;j>i;j--){ if(A[j-1].key>A[j].key){ swap(A[j-1],A[j]); flag=true; } } if(flag==false){ return; // 没有发生交换,结束 } } }复杂度分析 时间复杂度:$O(n^2)$,最坏情况下需要进行n次插入,每次插入需要移动O(n)个元素。平均也是$O(n^2)$。 空间复杂度:O(1),只使用了常数级别的额外空间。 稳定性:稳定 快速排序 思路 每次取一个基准元素pivot。每趟排序后,pivot位置确定。 过程 确定枢轴位置的过程: 枢轴图片 快排整体过程: 整体过程图片 代码 void QuickSort(ElemType A[], int low, int high) { if (low < high) { int pivot = Partition(A, low, high); QuickSort(A, low, pivot - 1); QuickSort(A, pivot + 1, high); } } int Partition(ElemType A[], int low, int high) { ElemType pivot = A[low]; while (low < high) { while (low < high && A[high] >= pivot) high--; A[low] = A[high]; while (low < high && A[low] <= pivot) low++; A[high] = A[low]; } A[low] = pivot; return low; }复杂度分析 时间复杂度:$O(n \log _2 n)$,平均情况下,快速排序的时间复杂度为 $O(n \log_2 n)$,最坏情况下为 $O(n^2)$。 空间复杂度:$O(\log_2 n)$,主要是递归调用栈的空间。 稳定性:不稳定。 简单选择排序 思路 假设排序表为$L[1...n]$ ,第i趟排序从$L[i...n]$中选择关键字最小的元素与L(i)交换。 代码 void SelectionSort(ElemType A[], int n) { for (int i = 1; i < n; i++) { int minIndex = i; for (int j = i + 1; j <= n; j++) { if (A[j] < A[minIndex]) { minIndex = j; } } swap(A[i], A[minIndex]); } }复杂度分析 时间复杂度:$O(n^2)$,最坏情况下需要进行n次选择,每次选择需要遍历O(n)个元素。 空间复杂度:O(1),只使用了常数级别的额外空间。 稳定性:不稳定。 堆排序 思路 将待排序的数组看作一个完全二叉树,只要满足了父节点大于等于子节点,就是大根堆,反之亦然,经常用此来实现优先队列 过程 自下而上调整为大根堆: 自下往上调整为大根堆图片 之后,把根节点与最后一个节点交换,然后再对除最后一个结点以外的所有元素进行调整,直到整个堆有序。 删除: 删除图片 插入: 插入图片 代码 代码不是那么重要哈~void HeapSort(ElemType A[], int n) { BuildMaxHeap(A, n); for (int i = n - 1; i > 0; i--) { swap(A[0], A[i]); MaxHeapify(A, 0, i); } } void BuildMaxHeap(ElemType A[], int n) { for (int i = n / 2 - 1; i >= 0; i--) { MaxHeapify(A, i, n); } } void MaxHeapify(ElemType A[], int i, int n) { int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; if (left < n && A[left] > A[largest]) largest = left; if (right < n && A[right] > A[largest]) largest = right; if (largest != i) { swap(A[i], A[largest]); MaxHeapify(A, largest, n); } }复杂度分析 时间复杂度:$O(n \log_2 n)$,主要是建堆和调整堆的时间复杂度。 空间复杂度:$O(1)$,只使用了常数级别的额外空间。 稳定性:不稳定。 归并排序 思路 二路归并:将待排序序列分为两部分,分别对这两部分进行归并排序,然后将已排序的两部分合并成一个整体有序序列。 过程 二路归并图片 代码 void MergeSort(ElemType A[], int left, int right) { if (left < right) { int mid = (left + right) / 2; MergeSort(A, left, mid); MergeSort(A, mid + 1, right); Merge(A, left, mid, right); } } void Merge(ElemType A[], int left, int mid, int right) { int i = left, j = mid + 1, k = 0; ElemType* temp = new ElemType[right - left + 1]; while (i <= mid && j <= right) { if (A[i] < A[j]) { temp[k++] = A[i++]; } else { temp[k++] = A[j++]; } } while (i <= mid) temp[k++] = A[i++]; while (j <= right) temp[k++] = A[j++]; for (i = left, k = 0; i <= right; i++, k++) { A[i] = temp[k]; } delete[] temp; }复杂度分析 时间复杂度:$O(n \log_2 n)$,主要是分割和合并的时间复杂度。 空间复杂度:$O(n)$,需要额外的空间来存放合并后的结果。 稳定性:稳定。 基数排序 思路 基数排序并不基于比较和移动进行排序,而是基于关键字的值进行排序,将所有数据收集到一个数组中,然后根据关键字的某一位进行排序,直到所有的关键字都排序完成。 为实现多关键字排序,通常有两种方法:第一种是最高位优先(MSD)法,按关键字位权重递减依次逐层划分成若干更小的子序列,最后将所有子序列依次连接成一个有序序列;第二种是最低位优先(LSD)法,按关键字位权重递增依次进行排序,最后形成一个有序序列。。 过程 通常采用链式基数排序,假设对如下10个记录进行排序:278 109 063 930 589 184 505 269 008 083 这个时候基数r=10,把每一个整数分为个位,十位,百位三个子关键字,进行三趟分配和收集,如下图所示: 基础排序过程图片 复杂度分析 空间复杂度:r个队列(r个队头指针,r个队尾指针),故为$O(r)$ 时间复杂度:d趟,每趟都要遍历整个数组,还要合并r个队列,故为$O(d(n+r))$ 稳定性:稳定 适用:顺序存储和链式存储的线性表。 计数排序 不在大纲内,但是思想很重要!思路 计数排序的基本思想是:对于待排序的数组,首先找出其中的最大值和最小值,然后统计每个元素出现的次数,最后根据统计结果将元素放回原数组中。 过程 找到待排序数组的最大值和最小值。 创建一个计数数组,大小为最大值与最小值之差加一,用于统计每个元素出现的次数。 遍历待排序数组,将每个元素的出现次数存入计数数组中。 根据计数数组的统计结果,将元素放回原数组中。 代码 void CountingSort(ElemType A[], int n) { if (n <= 0) return; // 找到最大值和最小值 ElemType maxVal = A[0]; ElemType minVal = A[0]; for (int i = 1; i < n; i++) { if (A[i] > maxVal) maxVal = A[i]; if (A[i] < minVal) minVal = A[i]; } // 创建计数数组 int range = maxVal - minVal + 1; int* count = new int[range](); for (int i = 0; i < n; i++) { count[A[i] - minVal]++; } // 将元素放回原数组 int index = 0; for (int i = 0; i < range; i++) { while (count[i] > 0) { A[index++] = i + minVal; count[i]--; } } delete[] count; }复杂度分析 时间复杂度:$O(n + k)$,其中 n 是待排序数组的长度,k 是计数数组的长度。 空间复杂度:$O(k)$,需要额外的空间来存放计数数组。 稳定性:稳定。 内部排序算法性能分析 算法种类最好情况平均情况最坏情况空间复杂度是否稳定每次能否固定一个位置比较次数与初始状态有关直接插入排序$O(n)$$O(n^2)$$O(n^2)$O(1)是否是冒泡排序$O(n)$$O(n^2)$$O(n^2)$O(1)是是是简单选择排序$O(n^2)$$O(n^2)$$O(n^2)$O(1)否是否希尔排序 O(1)否否是快速排序$O(nlog_2n)$$O(nlog_2n)$$O(n^2)$$O(log_2n)$否是是堆排序$O(nlog_2n)$$O(nlog_2n)$$O(nlog_2n)$$O(1)$否是是2路归并排序$O(nlog_2n)$$O(nlog_2n)$$O(nlog_2n)$$O(n)$是否-基数排序$O(d(n+2))$$O(d(n+r))$$O(d(n+r))$$O(r)$是否-外部排序 外部排序暂时不整理在一般情况下,对于 k–路平衡归并来说,若 (m-1)%(k-1)=0,则不需要增加虚段;否则需附加 k-(m-1)%(k-1)-1 个虚段。 -
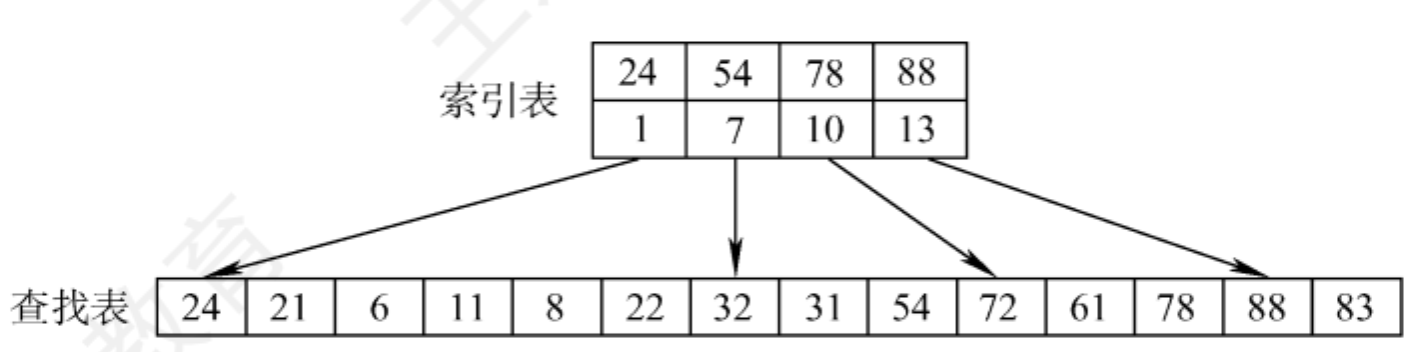
 【计算机考研(408)- 数据结构】查找 查找 查找长度——在查找运算中,需要对比关键字的次数称为查找长度。 平均查找长度(ASL, Average Search Length )—— 所有查找过程中进行的关键字的⽐较次数的平均值 顺序查找 思路:从头找到尾 代码实现: typedef struct { ElemType *elem; int TableLen;//表长 }SSTable; int Search_Seq(SSTable ST,ElemType key){ ST.elem[0]=key; for(i=ST.TableLen;ST.elem[i]!=key;--i); return i; }ST.elem[0]为哨兵:哨兵的作用是遍历时不会越界,即遍历到0时会退出。这要求由后向前遍历 $ALS_{\text{成功}}=\frac{(n+1)}{2}$;$ASL_{\text{不成功}}=n+1$ 线性链表只能顺序查找 有序表的顺序查找:不需查找完就可以退出。 $ASL_{成功}=\frac{(n+1)}{2}$;$ASL_{不成功}=\frac{n}{2}+\frac{n}{(n+1)}$ 折半查找 二分法,只适用于有序线性表 代码: int Binary_Search(SeqList L,ElemType key){ int low=0,high=L.TableLen-1,mid; while(low<=high){ mid=(low+high)/2; if(L.elem[mid]==key){ return mid; } else if(L.elem[mid]>key){ high=mid-1; }else{ low=mid+1; } } return -1; }ASL=$log_2(n+1)-1$ 分块查找 块内无序,块间有序 “索引表”中保存每个分块的最大关键字和分块的存储区间。 示意图如下所示: 分块查找示意图图片 设索引查找和块内查找的平均查找长度分别为LI、 LS,则分块查找的平均查找长度为 $$ ASL=L_I + L_S $$ 假设,⻓度为n的查找表被均匀地分为b块,每块s个元素 ⽤顺序查找查索引表: $$ ASL=\frac{s^2 + 2s + n}{2s} $$ 当 $s=\sqrt{n}$ 时,分块查找的平均查找长度达到最优。$ASL_{最小}=\sqrt{n} +1$ ⽤折半查找查索引表: 用折半查找查索引表时,平均查找长度为: $$ ASL = \lceil \log_2(b + 1) \rceil + \frac{s+1}{2} $$树形查找 二叉排序树 定义 二叉排序树,又称二叉查找树(BST,Binary Search Tree)一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树: 左子树上所有结点的关键字均小于根结点的关键字; 右子树上所有结点的关键字均大于根结点的关键字。 左子树和右子树又各是一棵二叉排序树。 所以:左子树结点值< 根结点值< 右子树结点值 所以:进行中序遍历,可以得到一个递增的有序序列 查找过程 若树非空,目标值与根结点的值比较:若相等,则查找成功;若小于根结点,则在左子树上查找,否则在右子树上查找。查找成功,返回结点指针;查找失败返回NULL 相关操作及实现 结点定义: typedef struct BSTNode{ int data; struct BSTNode *lchild, *rchild; }BSTNode,*BSTree;查找: //非递归 BSTNode *Search(BSTree T, int key){ while(T!=NULL && key!=T->data){ if(key < T->data) T = T->lchild; else T = T->rchild; } return T; } //递归 BSTNode *Search(BSTree T, int key){ if(T==NULL || key==T->data) return T; if(key < T->data) return Search(T->lchild, key); return Search(T->rchild, key); }插入: 若原二叉排序树为空,则直接插入结点;否则,若关键字k小于根结点值,则插入到左子树,若关键字k大于根结点值,则插入到右子树 bool Insert(BSTree &T, int key){ if(T==NULL){ T = (BSTNode *)malloc(sizeof(BSTNode)); T->data = key; T->lchild = T->rchild = NULL; return true; } else if(key == T->data) return false;//树中存在相同关键字的结点,插入失败 else if(key < T->data) return Insert(T->lchild, key); else return Insert(T->rchild, key); }不同的关键字序列可能得到同款二叉排序树,也可能得到不同款二叉排序树删除: 先找到被删除的结点z 若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质 若结点z只有一棵左子树或右子树,则让z的子树成为z父结点的子树,替代z的位置。 若结点z有左、右两棵子树,则令z的直接后继(或直接前驱)替代z,然后从二叉排序树中删去这个直接后继(或直接前驱),这样就转换成了第一或第二种情况 直接后继:z的右子树中最左下结点,直接前驱:z的左子树中最右下结点如下图所示三种情况的删除操作: 三种情况的删除操作图片 复杂度分析 最好情况:n个结点的二叉树最小高度为$(\lfloor log_2n \rfloor+1)$。平均查找长度= $O(log_2n)$ 最坏情况:每个结点只有一个分支,树高h=结点数n。平均查找长度=O(n)。 需要借助[[#平衡二叉树]]来解决达到平均查找长度为$O(log_2n)$。 平衡二叉树 定义 平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树) 树上任一结点的左子树和右子树的高度之差不超过1。结点的平衡因子=左子树高-右子树高。 相关操作 插入:在插入过程中可能会破坏平衡,因此需要重新平衡。 在插入操作中,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡。 时刻记住:二叉排序树的特性:左子树结点值< 根结点值< 右子树结点值分为以下四种情况: 1)LL平衡旋转(右单旋转)。由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。 LL图片 2)RR平衡旋转(左单旋转)。由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A结点的右子树 RR图片 3)LR平衡旋转(先左后右双旋转)。由于在A的左孩子(L)的右子树(R)上插入新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置,然后再把该C结点向右上旋转提升到A结点的位置 LR图片 4)RL平衡旋转(先右后左双旋转)。由于在A的右孩子(R)的左子树(L)上插入新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置 RL图片 删除: 平衡二叉树的删除操作具体步骤: 删除结点(方法同“二叉排序树”) 一路向北找到最小不平衡子树,找不到就完结撒花 找最小不平衡子树下,“个头”最高的儿子、孙子 根据孙子的位置,调整平衡(LL/RR/LR/RL) 孙子在LL:儿子右单旋 孙子在RR:儿子左单旋 孙子在LR:孙子先左旋,再右旋 孙子在RL:孙子先右旋,再左旋 如果不平衡向上传导,继续一路向北! 删除操作举例: 平衡二叉树的删除图片 复杂度分析 平衡二叉树删除操作时间复杂度=$O(log_2n)$ 这里其实会有一个红黑树的,但是难度有点高,我就不在这里整理了,等以后有力气学的时候再学B树 B树中所有结点的孩子结点数的最大值称为B树的阶。一棵m阶树或为空树,或满足如下特征的m叉树: 树中每个结点至多有m棵子树,即至多含m-1个关键字 若根结点不是终端结点,则至少有两棵子树 除根结点外的所有非叶结点至少有$\lceil m/2\rceil$棵子树,即至少$\lceil m/2\rceil -1$个关键字 非叶结点关键字递减,且关键字左子树小于该关键字,右子树大于该关键字 所有叶结点在同一层,不带信息 B树是所有结点平衡因子都为0的多路查找树。 B树示例: B树图片 B树的结点插入示例(3阶B树): B树的结点插入示例图片 删除示例: B删除示例1图片 B删除示例2图片 B+ 树 B与B+树的区别 在B+树中,n个关键字的结点含有n棵子树,即每个关键字对应一棵子树。而B树中,具有n个关键字的结点含有n+1棵子树 在B+树种,每个结点的关键字个数n的范围是$\lceil m/2\rceil <=n<= m$(根结点1<=n<=n);在B树中,每个结点的关键字个数n的范围是$\lceil m/2 \rceil -1<=n<=n-1$,(根结点1<=n<=m-1) 在B+树中,叶结点包含信息,所有非叶结点仅起索引作用,非叶结点中的每个索引项只含有相应子树的最大关键字和指向该子树的指针,不含该关键字对应记录的存储地址 在B+树中,叶结点包含了全部关键字,即在非叶结点种出现的关键字也会出现在叶结点中;而在B树中,叶结点包含的关键字和其他结点包含的关键字是不重复的。 B+树示意图图片 散列表 定义 散列表(哈希表,Hash Table) :是⼀种数据结构。 特点是:可以根据数据元素的关键字计算出它在散列表中的存储地址 散列函数(哈希函数) :Addr=H(key) 建⽴了“关键字”→“存储地址”的映射关系 构造方法 直接定址法:$H(key) = a \times key + b$,其中 $a, b$ 为常数。最简单且无冲突,适用于关键字分布基本连续的情况。若关键字分布不连续,空位较多,会造成空间浪费。 除留余数法:$H(key) = key \bmod p$,其中 $p$ 是一个不大于 $m$(散列表长度)但接近于 $m$ 的质数。 数字分析法 —— 选取数码分布较为均匀的若⼲位作为散列地址,设关键字是r进制数(如⼗进制数),而r个数码在各位上出现的频率不⼀定相同,可能在某些位上分布均匀⼀些,每种数码出现的机会均等;⽽在某些位上分布不均匀,只有某⼏种数码经常出现,此时可选取数码分布较为均匀的若⼲位作为散列地址。 平⽅取中法——取关键字的平⽅值的中间⼏位作为散列地址。具体取多少位要视实际情况⽽定。 这种⽅法得到的散列地址与关键字的每位都有关系,因此使得散列地址分布⽐较均匀。 处理冲突的方法 线性探测法 $d_i=0,1,2,...,m-1$,发生冲突时,找到一个空闲空间,看看下一个。容易产生堆积现象 平方探测法 $d_i=0^2,1^2,-1^2,2^2,-2^2,...,k^2,-k^2$,k<=m/2.散列表长度m必须是一个可以表示成4k+3的素数。能解决堆积现象,但不能探测到散列表的所有单元 再散列法 $d_i=Hash_2(key)$,再通过另外一个散列函数计算关键字的地址增量。$H_i=(H(key)+i*Hash_2(key))\%m$,i是冲突次数,初始时为0. 拉链法 如果将所有同义词存储在一个线性链表中,那么在查找时只需遍历该链表即可找到所有同义词。假设有关键词序列{19,14,23,01,68,20,84,27,55,11,10,79},散列函数$H(key)=key\%13$,所建立的表如下图所示: 拉链法处理冲突的散列表图片 散列表查找及性能分析 $\alpha=\frac{表中记录数n}{散列表长度m}$,散列表的平均查找长度依赖于散列表的装填因子$\alpha$,而不直接依赖于n或m。$\alpha$越大,冲突的可能性越大。 串的模式匹配算法 也就是KMP算法!由于这一章节相对独立而且相对来说比较复杂,难度并不高,所以在第二轮复习的过程中我没有整理KMP算法,考场上直接暴力解也不是不行,所以等着以后和红黑树一起来整理。计算next。 前一个next为n时,匹配前面串前n与后n是否相同,相同这个next是n+1,不同的话就-1,再匹配,匹配到相同后+1,以此类推。 如何求Next数组图片 计算next,就是看当前字符前的子串前后相同的长度,若由0开始,则next[i]=前后相同长度+1,若由-1开始,next[i]=前后相同长度。nextval第一个是和next值一样,后面的话对比a[next[i]],如果相同的话,nextval[i]=nextval[next[i]],就是两个一样,如果不同的话,nextval[i]=next[i],这个nextval的作用和next一样,只不过是加强版,能更快。都是用来比较用的。
【计算机考研(408)- 数据结构】查找 查找 查找长度——在查找运算中,需要对比关键字的次数称为查找长度。 平均查找长度(ASL, Average Search Length )—— 所有查找过程中进行的关键字的⽐较次数的平均值 顺序查找 思路:从头找到尾 代码实现: typedef struct { ElemType *elem; int TableLen;//表长 }SSTable; int Search_Seq(SSTable ST,ElemType key){ ST.elem[0]=key; for(i=ST.TableLen;ST.elem[i]!=key;--i); return i; }ST.elem[0]为哨兵:哨兵的作用是遍历时不会越界,即遍历到0时会退出。这要求由后向前遍历 $ALS_{\text{成功}}=\frac{(n+1)}{2}$;$ASL_{\text{不成功}}=n+1$ 线性链表只能顺序查找 有序表的顺序查找:不需查找完就可以退出。 $ASL_{成功}=\frac{(n+1)}{2}$;$ASL_{不成功}=\frac{n}{2}+\frac{n}{(n+1)}$ 折半查找 二分法,只适用于有序线性表 代码: int Binary_Search(SeqList L,ElemType key){ int low=0,high=L.TableLen-1,mid; while(low<=high){ mid=(low+high)/2; if(L.elem[mid]==key){ return mid; } else if(L.elem[mid]>key){ high=mid-1; }else{ low=mid+1; } } return -1; }ASL=$log_2(n+1)-1$ 分块查找 块内无序,块间有序 “索引表”中保存每个分块的最大关键字和分块的存储区间。 示意图如下所示: 分块查找示意图图片 设索引查找和块内查找的平均查找长度分别为LI、 LS,则分块查找的平均查找长度为 $$ ASL=L_I + L_S $$ 假设,⻓度为n的查找表被均匀地分为b块,每块s个元素 ⽤顺序查找查索引表: $$ ASL=\frac{s^2 + 2s + n}{2s} $$ 当 $s=\sqrt{n}$ 时,分块查找的平均查找长度达到最优。$ASL_{最小}=\sqrt{n} +1$ ⽤折半查找查索引表: 用折半查找查索引表时,平均查找长度为: $$ ASL = \lceil \log_2(b + 1) \rceil + \frac{s+1}{2} $$树形查找 二叉排序树 定义 二叉排序树,又称二叉查找树(BST,Binary Search Tree)一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树: 左子树上所有结点的关键字均小于根结点的关键字; 右子树上所有结点的关键字均大于根结点的关键字。 左子树和右子树又各是一棵二叉排序树。 所以:左子树结点值< 根结点值< 右子树结点值 所以:进行中序遍历,可以得到一个递增的有序序列 查找过程 若树非空,目标值与根结点的值比较:若相等,则查找成功;若小于根结点,则在左子树上查找,否则在右子树上查找。查找成功,返回结点指针;查找失败返回NULL 相关操作及实现 结点定义: typedef struct BSTNode{ int data; struct BSTNode *lchild, *rchild; }BSTNode,*BSTree;查找: //非递归 BSTNode *Search(BSTree T, int key){ while(T!=NULL && key!=T->data){ if(key < T->data) T = T->lchild; else T = T->rchild; } return T; } //递归 BSTNode *Search(BSTree T, int key){ if(T==NULL || key==T->data) return T; if(key < T->data) return Search(T->lchild, key); return Search(T->rchild, key); }插入: 若原二叉排序树为空,则直接插入结点;否则,若关键字k小于根结点值,则插入到左子树,若关键字k大于根结点值,则插入到右子树 bool Insert(BSTree &T, int key){ if(T==NULL){ T = (BSTNode *)malloc(sizeof(BSTNode)); T->data = key; T->lchild = T->rchild = NULL; return true; } else if(key == T->data) return false;//树中存在相同关键字的结点,插入失败 else if(key < T->data) return Insert(T->lchild, key); else return Insert(T->rchild, key); }不同的关键字序列可能得到同款二叉排序树,也可能得到不同款二叉排序树删除: 先找到被删除的结点z 若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质 若结点z只有一棵左子树或右子树,则让z的子树成为z父结点的子树,替代z的位置。 若结点z有左、右两棵子树,则令z的直接后继(或直接前驱)替代z,然后从二叉排序树中删去这个直接后继(或直接前驱),这样就转换成了第一或第二种情况 直接后继:z的右子树中最左下结点,直接前驱:z的左子树中最右下结点如下图所示三种情况的删除操作: 三种情况的删除操作图片 复杂度分析 最好情况:n个结点的二叉树最小高度为$(\lfloor log_2n \rfloor+1)$。平均查找长度= $O(log_2n)$ 最坏情况:每个结点只有一个分支,树高h=结点数n。平均查找长度=O(n)。 需要借助[[#平衡二叉树]]来解决达到平均查找长度为$O(log_2n)$。 平衡二叉树 定义 平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树) 树上任一结点的左子树和右子树的高度之差不超过1。结点的平衡因子=左子树高-右子树高。 相关操作 插入:在插入过程中可能会破坏平衡,因此需要重新平衡。 在插入操作中,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡。 时刻记住:二叉排序树的特性:左子树结点值< 根结点值< 右子树结点值分为以下四种情况: 1)LL平衡旋转(右单旋转)。由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。 LL图片 2)RR平衡旋转(左单旋转)。由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点,将A结点向左下旋转成为B的左子树的根结点,而B的原左子树则作为A结点的右子树 RR图片 3)LR平衡旋转(先左后右双旋转)。由于在A的左孩子(L)的右子树(R)上插入新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置,然后再把该C结点向右上旋转提升到A结点的位置 LR图片 4)RL平衡旋转(先右后左双旋转)。由于在A的右孩子(R)的左子树(L)上插入新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置 RL图片 删除: 平衡二叉树的删除操作具体步骤: 删除结点(方法同“二叉排序树”) 一路向北找到最小不平衡子树,找不到就完结撒花 找最小不平衡子树下,“个头”最高的儿子、孙子 根据孙子的位置,调整平衡(LL/RR/LR/RL) 孙子在LL:儿子右单旋 孙子在RR:儿子左单旋 孙子在LR:孙子先左旋,再右旋 孙子在RL:孙子先右旋,再左旋 如果不平衡向上传导,继续一路向北! 删除操作举例: 平衡二叉树的删除图片 复杂度分析 平衡二叉树删除操作时间复杂度=$O(log_2n)$ 这里其实会有一个红黑树的,但是难度有点高,我就不在这里整理了,等以后有力气学的时候再学B树 B树中所有结点的孩子结点数的最大值称为B树的阶。一棵m阶树或为空树,或满足如下特征的m叉树: 树中每个结点至多有m棵子树,即至多含m-1个关键字 若根结点不是终端结点,则至少有两棵子树 除根结点外的所有非叶结点至少有$\lceil m/2\rceil$棵子树,即至少$\lceil m/2\rceil -1$个关键字 非叶结点关键字递减,且关键字左子树小于该关键字,右子树大于该关键字 所有叶结点在同一层,不带信息 B树是所有结点平衡因子都为0的多路查找树。 B树示例: B树图片 B树的结点插入示例(3阶B树): B树的结点插入示例图片 删除示例: B删除示例1图片 B删除示例2图片 B+ 树 B与B+树的区别 在B+树中,n个关键字的结点含有n棵子树,即每个关键字对应一棵子树。而B树中,具有n个关键字的结点含有n+1棵子树 在B+树种,每个结点的关键字个数n的范围是$\lceil m/2\rceil <=n<= m$(根结点1<=n<=n);在B树中,每个结点的关键字个数n的范围是$\lceil m/2 \rceil -1<=n<=n-1$,(根结点1<=n<=m-1) 在B+树中,叶结点包含信息,所有非叶结点仅起索引作用,非叶结点中的每个索引项只含有相应子树的最大关键字和指向该子树的指针,不含该关键字对应记录的存储地址 在B+树中,叶结点包含了全部关键字,即在非叶结点种出现的关键字也会出现在叶结点中;而在B树中,叶结点包含的关键字和其他结点包含的关键字是不重复的。 B+树示意图图片 散列表 定义 散列表(哈希表,Hash Table) :是⼀种数据结构。 特点是:可以根据数据元素的关键字计算出它在散列表中的存储地址 散列函数(哈希函数) :Addr=H(key) 建⽴了“关键字”→“存储地址”的映射关系 构造方法 直接定址法:$H(key) = a \times key + b$,其中 $a, b$ 为常数。最简单且无冲突,适用于关键字分布基本连续的情况。若关键字分布不连续,空位较多,会造成空间浪费。 除留余数法:$H(key) = key \bmod p$,其中 $p$ 是一个不大于 $m$(散列表长度)但接近于 $m$ 的质数。 数字分析法 —— 选取数码分布较为均匀的若⼲位作为散列地址,设关键字是r进制数(如⼗进制数),而r个数码在各位上出现的频率不⼀定相同,可能在某些位上分布均匀⼀些,每种数码出现的机会均等;⽽在某些位上分布不均匀,只有某⼏种数码经常出现,此时可选取数码分布较为均匀的若⼲位作为散列地址。 平⽅取中法——取关键字的平⽅值的中间⼏位作为散列地址。具体取多少位要视实际情况⽽定。 这种⽅法得到的散列地址与关键字的每位都有关系,因此使得散列地址分布⽐较均匀。 处理冲突的方法 线性探测法 $d_i=0,1,2,...,m-1$,发生冲突时,找到一个空闲空间,看看下一个。容易产生堆积现象 平方探测法 $d_i=0^2,1^2,-1^2,2^2,-2^2,...,k^2,-k^2$,k<=m/2.散列表长度m必须是一个可以表示成4k+3的素数。能解决堆积现象,但不能探测到散列表的所有单元 再散列法 $d_i=Hash_2(key)$,再通过另外一个散列函数计算关键字的地址增量。$H_i=(H(key)+i*Hash_2(key))\%m$,i是冲突次数,初始时为0. 拉链法 如果将所有同义词存储在一个线性链表中,那么在查找时只需遍历该链表即可找到所有同义词。假设有关键词序列{19,14,23,01,68,20,84,27,55,11,10,79},散列函数$H(key)=key\%13$,所建立的表如下图所示: 拉链法处理冲突的散列表图片 散列表查找及性能分析 $\alpha=\frac{表中记录数n}{散列表长度m}$,散列表的平均查找长度依赖于散列表的装填因子$\alpha$,而不直接依赖于n或m。$\alpha$越大,冲突的可能性越大。 串的模式匹配算法 也就是KMP算法!由于这一章节相对独立而且相对来说比较复杂,难度并不高,所以在第二轮复习的过程中我没有整理KMP算法,考场上直接暴力解也不是不行,所以等着以后和红黑树一起来整理。计算next。 前一个next为n时,匹配前面串前n与后n是否相同,相同这个next是n+1,不同的话就-1,再匹配,匹配到相同后+1,以此类推。 如何求Next数组图片 计算next,就是看当前字符前的子串前后相同的长度,若由0开始,则next[i]=前后相同长度+1,若由-1开始,next[i]=前后相同长度。nextval第一个是和next值一样,后面的话对比a[next[i]],如果相同的话,nextval[i]=nextval[next[i]],就是两个一样,如果不同的话,nextval[i]=next[i],这个nextval的作用和next一样,只不过是加强版,能更快。都是用来比较用的。 -
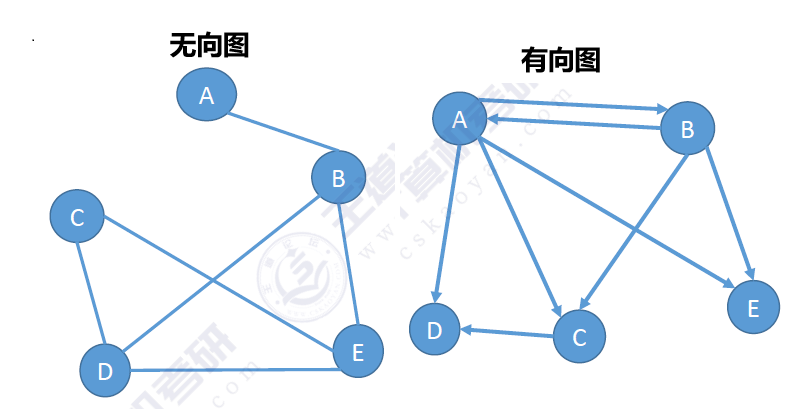
 【计算机考研(408)- 数据结构】图 图 图的定义 图 $G$ 由顶点集 $V$ 和边集 $E$ 组成,记为 $G = (V, E)$,其中 $V(G)$ 表示图 $G$ 中顶点的有限非空集,$E(G)$ 表示图 $G$ 中顶点之间的关系(边)集合。若 $V = \{v_1, v_2, \ldots, v_n\}$,则用 $|V|$ 表示图 $G$ 中顶点的个数(称为图的阶),$E = \{(u, v) \mid u \in V, v \in V\}$,用 $|E|$ 表示图 $G$ 中边的条数。 线性表可以是空表,树可以是空树,但是图不能是空图,即使他没有边,他也不能没有顶点,也就是说图中不能一个定点都没有,但边集E可以为空。 G:Graph V:Vertex E:Edge来点题外话:假设南昌东站、昌北机场站、共青城东站、庐山东站是一个个顶点V,那么连接他们之间的铁路可以看作是边E,那么构成的图G就是一张图。也就是京港高铁昌九段,在延申一点就是全国高铁网络均可看作是一张大图。 有关图的相关概念 有向图和无向图 有向图:若 $E$ 是有向边(弧)的有限集合,则图 $G$ 为有向图。弧是顶点的有序对,记为 $\langle v, w \rangle$,其中 $v$、$w$ 是顶点,$v$ 称为弧尾,$w$ 称为弧头,$\langle v, w \rangle$ 表示从顶点 $v$ 到顶点 $w$ 的弧。$\langle v, w \rangle \ne \langle w, v \rangle$。 无向图:若 $E$ 是无向边(边)的有限集合,则图 $G$ 为无向图。无向边是顶点的无序对,记为 $(v, w)$ 或 $(w, v)$,其中 $v$、$w$ 是顶点,且 $(v, w) = (w, v)$。 示例: 有向图 $G_1 = (V_1, E_1)$ $V_1 = \{A, B, C, D, E\}$ $E_1 = \{\langle A, B \rangle, \langle A, C \rangle, \langle A, D \rangle, \langle A, E \rangle, \langle B, A \rangle, \langle B, C \rangle, \langle B, E \rangle, \langle C, D \rangle\}$ 无向图 $G_2 = (V_2, E_2)$ $V_2 = \{A, B, C, D, E\}$ $E_2 = \{(A, B), (B, D), (B, E), (C, D), (C, E), (D, E)\}$ 有向图无向图示例图片 简单图和多重图 简单图:满足不存在重复边,不存在顶点到自身的边。数据结构只讨论简单图。 多重图:两个结点的边数多余一条,且允许有顶点到自身的边。与简单图相对。 简单图/多重图图片 顶点的度 无向图 顶点的度:一个顶点的度等于依附于该顶点的边的条数。记作$TD(v)$ 所有顶点的度之和等于边数的两倍。 在具有n个顶点,e条边的无向图图,$\sum^n_{i=1}TD(v_i)=2e$ 有向图 入度:以该顶点为终点的有向边的条数。记作$ID(v)$ 出度:以该顶点为起点的有向边的条数。记作$OD(v)$ 顶点的度 = 入度 + 出度。$TD(v)=ID(v)+OD(v)$ 所有顶点的入度之和等于所有顶点的出度之和,且都等于边的总数。 在具有n个顶点,e条边的有向图,$\sum^n_{i=1}ID(v_i)=\sum^n_{i=1}OD(v_i)=e$ 顶点之间的关系的描述 路径:顶点 $v_p$ 到顶点 $v_q$ 之间的一条路径是指顶点序列,$v_p, v_{i_1}, v_{i_2}, \ldots, v_{i_m}, v_q$ 。 回路:第一个顶点和最后一个顶点相同的路径称为回路或环。$v_p, v_{i_1}, v_{i_2}, \ldots, v_{i_m}, v_p$ 。 简单路径:在路径序列中,顶点不重复出现的路径称为简单路径。 简单回路:除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。 路径长度:路径上边的数目。 点到点的距离:从顶点 $u$ 出发到顶点 $v$ 的最短路径(若存在),此路径的长度称为从 $u$ 到 $v$ 的距离。若从 $u$ 到 $v$ 根本不存在路径,则记该距离为无穷($\infty$)。 若一个图有n个顶点,且边数大于n-1,则此图一定有环。 在有向图中,如果从顶点v到顶点w和从顶点w到顶点v都有路径,则称这两个顶点是强连通的。 在无向图中,如果从顶点v到顶点w有路径存在,则称这两个顶点是连通的。 图的连通性(连通图、强连通图) 连通图:若图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。 对于有 $n$ 个顶点的无向图 $G$,若 $G$ 是连通图,则最少有 $n-1$ 条边。若 $G$ 是非连通图,则最多可能有$C_{n-1}^2$条边。 强连通图:若图中任何一对顶点都是强连通的,则称此图为强连通图。 对于有 $n$ 个顶点的有向图 $G$,若 $G$ 是强连通图,则最少有$n$条边(形成回路)。 连通分量:无向图中的极大连通子图([[#子图]]必须连通,且包含尽可能多的顶点和边)称为连通分量。 说句题外的例子:如果我们把刚刚拓展到全国铁路网看作是一张图G,那么相应的京港高速铁路昌九段就是一个子图,那么相应的,大陆地区/台湾地区/海南省的铁路网就是这张图的连通分量。 强连通分量:有向图 $G$ 中的极大强连通子图([[#子图]]必须强连通,且包含尽可能多的顶点和边)称为强连通分量。 子图 子图:设有两个图 $G = (V, E)$ 和 $G' = (V', E')$,若 $V' \subseteq V$ 且 $E' \subseteq E$,则称 $G'$ 是 $G$ 的子图。若 $V(G') = V(G)$,则称 $G'$ 为 $G$ 的生成子图(即包含全部顶点的子图)。 生成树&生成森林 连通图的生成树是包含全部顶点的极小连通子图(边要尽可能地少,但要保持连通)。若顶点为n,则有n-1条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。 在非连通图中,连通分量的生成树构成非连通图的生成森林。 边的权、带权图 边的权:在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。 带权图(网):边上带有权值的图称为带权图,也称网。 带权路径长度:当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度。 ^Cite1 还是上面的例子,如果我们在每个边上表明两个车站之间的距离,那么这个图就是带权图。 几种特殊的图 无向完全图:无向图中任意两个顶点之间都存在边。 若无向图的顶点数 $|V| = n$,则边的数目 $|E|$ 的取值范围为 $0 \leq |E| \leq \frac{n(n-1)}{2}$ 。(即$C_n^2$) 有向完全图:有向图中任意两个顶点之间都存在方向相反的两条弧。 若有向图的顶点数$|V|=n$,则弧的数目 $|E|$ 的取值范围为 $0 \leq |E| \leq n(n-1)$ 。(即$2C_n^2$) 稀疏图:边数很少的图。反之称为稠密图。 注意,以上没有一个绝对的界限,一般来说$|E| < |V|log|V|$时,可以将G视为稀疏图 有向树:一个顶点的入度为0、其余顶点的入度为1的有向图,称为有向树。 树,不存在回路且连通的无向图,n个顶点的树有n-1条边。图的存储 邻接矩阵法 定义 邻接矩阵是指用一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息(各顶点间的邻接关系),存储顶点之间邻接关系的二维数组称为邻接矩阵。 结点数为$n$的图$G = (V, E)$的邻接矩阵A是$n*n$的。将G的顶点编号为$v_1, v_2, \ldots, v_n$,则: $$ A[i][j] = \begin{cases} 1, & \text{若}(v_i, v_j)\text{或}<v_i,v_j>\text{是E(G)中的边} \\ 0, & \text{若}(v_i, v_j)\text{或}<v_i,v_j>\text{不是E(G)中的边} \end{cases} $$以下是图的邻接矩阵示意图: 图的邻接矩阵示例图片 以下是带权图(网的)的邻接矩阵示意图: 带权图的邻接矩阵示例图片 对角线元素也经常用0表示代码实现 //图的邻接矩阵 #define MaxVertexNum 100 // 顶点数目的最大值 typedef struct{ char Vex[MaxVertexNum];//顶点表(这里可以拓展,存更多的信息) int Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵(当然也可以是bool型) int vexnum,edgenum;//顶点数和边数 }MGraph;//带权图的邻接矩阵(同时也对其进行了一定的拓展) #define MaxVertexNum 100 // 顶点数目的最大值 #define INFINITY MAX_INT //无穷大 typedef char VertexType;//顶点类型 tyepedef int EdgeType;//边的权值类型 typedef struct{ VertexType Vex[MaxVertexNum];//顶点表(这里可以拓展,存更多的信息) EdgeType Edge[MaxVertexNum][MaxVertexNum];//这里需要存储边的权值 int vexnum,edgenum;//顶点数和边数 }MGraph;特点 对无向图,第i个结点的度$TD(i)$=第i行(或第i列)非零元素的个数 对有向图,第i个结点的入度$ID(i)$=第i行非零元素(或非∞元素)的个数 对有向图,第i个结点的出度$OD(i)$=第i列非零元素(或非∞元素)的个数 第i个结点的度=第i行、第i列的非零元素个数之和 对于无向图的邻接矩阵一定是一个[[数组和特殊矩阵#对称矩阵]],所以在实际存储邻接矩阵的时候只需要存储上(或下)三角矩阵的元素。 稠密图适合用此方法表示。 设图G的邻接矩阵为A(矩阵元素为0/1),则$A^n$的元素$A^n[i][j]$等于由顶点i到顶点j的长度为n的路径的数目。 复杂度分析 空间复杂度:$O(|V|^2)$ ,其只和顶点数相关,和实际的边数无关 邻接矩阵法求顶点的度/出度/入度的时间复杂度:$O(|V|)$ 适合用于存储稠密图 无向图的邻接矩阵是对称矩阵,可以压缩存储(只存储上三角区/下三角区) 邻接表法 定义 邻接表,对图G中的每个顶点$v_i$建立一个单链表,第i个单链表中的结点表示依附于顶点$v_i$的边(对于有向图而言则是以顶点$v_i$为尾的弧,假设1->2,则挂在1上),这个单链表就是顶点$v_i$的边表(有向图中叫做出边表)。边表的头指针和顶点的数据信息采用顺序存储,称为顶点表,所以在邻接表中存在两种结点,顶点表结点和边表结点。 如下图所示,即为顶点表和边表的结点结构 顶点表和边表的数据结构图片 顶点表结点由顶点信息(存储顶点相关信息)和边表头指针(指向第一条边的边表结点)组成,边表结点由邻接点域(存储头结点顶点邻接的顶点编号)和指针域(指向下一条的边表结点)组成。 如图所示是有向图和无向图邻接表表示法的示例: 有向图和无向图邻接表表示法示例图片 代码实现 #define MaxVertexNum 100 // 最大顶点数 typedef struct ArcNode{ //边表结点 int adjvex; // 该弧指向的顶点的位置 struct ArcNode *next; // 指向下一条边的指针 // 其他信息(如权值等)可以在此处添加 } ArcNode; typedef struct VNode{ //顶点表结点 VertexType data; // 顶点信息 ArcNode *first; // 指向第一条弧的指针 } VNode,AdjList[MaxVertexNum]; typedef struct{ AdjList vertices; //邻接表 int vexnum,arcnum; //顶点数和弧数 } ALGraph;特点 适用于稀疏图 表示不唯一 复杂度分析 空间复杂度:$O(|V| + |E|)$(有向图),$O(|V| + 2|E|)$(无向图),其和顶点数、边数相关。 对于稀疏图,邻接表法比邻接矩阵法更节省空间。 十字链表法 十字链表是有向图的一种存储结构,十字链表中,每个弧有个结点,每个顶点也有一个结点。 下面是一个弧节点和顶点结点的示意图: 弧节点和顶点结点的示意图图片 以下是一个十字链表存储有向图的示意图: 十字链表存储有向图的示意图图片 空间复杂度:$O(|V| + |E|)$ 沿着绿色线路则是出边 沿着橙色线路则是入边 只能存储有向图 十字链表表示是不唯一的,但是一个十字链表表示唯一确定的一个图。 邻接多重表 邻接多重表是无向图的一种链式存储结构。与十字链表类似的是其边也用一个结点表示, 下面是一个邻接多重表的边节点和顶点结点的示意图: 邻接多重表的边节点和顶点结点的示意图图片 以下是一个邻接多重表存储无向图的示意图: 邻接多重表存储无向图的示意图图片 空间复杂度:$O(|V| + |E|)$ 只存储无向图 图的存储四种方法对比 属性邻接矩阵邻接表十字链表邻接多重表空间复杂度$O(\vert V\vert^2)$无向图 $O(\vert V\vert + 2\vert E\vert)$,有向图 $O(\vert V\vert + \vert E\vert)$$O(\vert V\vert + \vert E\vert)$$O(\vert V\vert + \vert E\vert)$找相邻边遍历对应行或列时间复杂度为$O(\vert V\vert)$找有向图的入边必须遍历整个邻接表很方便很方便删除边或顶点删除边很方便,删除顶点需要大量移动数据无向图中删除边或顶点都不方便很方便很方便适用于稠密图稀疏图和其他只能存有向图只能存无向图表示方式唯一不唯一不唯一不唯一图的基本操作 Adjacent(G, x, y) 判断图 $G$ 是否存在边 $\langle x, y \rangle$ 或 $(x, y)$。 Neighbors(G, x) 列出图 $G$ 中与结点 $x$ 邻接的所有顶点。 InsertVertex(G, x) 在图 $G$ 中插入顶点 $x$。 DeleteVertex(G, x) 从图 $G$ 中删除顶点 $x$ 及其相关的所有边。 AddEdge(G, x, y) 若无向边 $(x, y)$ 或有向边 $\langle x, y \rangle$ 不存在,则向图 $G$ 中添加该边。 RemoveEdge(G, x, y) 若无向边 $(x, y)$ 或有向边 $\langle x, y \rangle$ 存在,则从图 $G$ 中删除该边。 FirstNeighbor(G, x) 求图 $G$ 中顶点 $x$ 的第一个邻接点,若有则返回顶点号;若 $x$ 没有邻接点或图中不存在 $x$,则返回 $-1$。 NextNeighbor(G, x, y) 假设图 $G$ 中顶点 $y$ 是顶点 $x$ 的一个邻接点,返回除 $y$ 之外顶点 $x$ 的下一个邻接点的顶点号;若 $y$ 是 $x$ 的最后一个邻接点,则返回 $-1$。 Get_edge_value(G, x, y) 获取图 $G$ 中边 $(x, y)$ 或 $\langle x, y \rangle$ 对应的权值。 Set_edge_value(G, x, y, v) 设置图 $G$ 中边 $(x, y)$ 或 $\langle x, y \rangle$ 的权值为 $v$。 除此之外,还有[[#图的遍历|图的遍历]]相关操作。 图的遍历 广度优先搜索 广度优先搜索(BFS,Breadth-First Search)会优先考虑最早被发现的顶点,也就是说离起点越近的顶点其优先级越高。 基本思想 类似于二叉树的层序遍历。基本思想是:首先访问起始顶点v,接着由v出发,依次访问v的各个未访问过的邻接顶点$w_1,w_2,...,w_i$,然后依次访问$w_1,w_2,...,w_i$的所有未被访问过的邻接顶点;再从这些访问过的顶点出发,访问它们所有未被访问过的邻接顶点……。 为了实现逐层访问,必须借助一个辅助队列,用来记忆正在访问的顶点的下一层顶点。 代码实现 bool Visited[MAX_VERTEX_NUM]; // 访问标记数组 void BFSTraverse(Graph G) { for(int i = 0; i < G.vexnum; i++){ Visited[i] = false; // 初始化访问标记数组 } InitQueue(Q); for(int i = 0; i < G.vexnum; i++){//这里为了保证此图如果是一个非连通图,也能达成目的 if(!Visited[i]){ BFS(G, i); } } } //用邻接表实现的广度优先搜索算法 void BFS(ALGraph G, int i) { visit(i);//对i号结点访问 Visited[i] = true; // 标记i号结点已访问 EnQueue(Q, i); // 将i号结点入队 while(!QueueEmpty(Q)) { DeQueue(Q, v); // 队头结点出队 for(p=G.vertices[v].first; p!=NULL;p=p->next){// 遍历v的边表 w=p->adjvex; // 获取邻接点 if(!Visited[w]){ // 如果邻接点未访问 visit(w); // 访问邻接点 Visited[w] = true; // 标记邻接点已访问 EnQueue(Q, w); // 将邻接点入队 } } } } //使用邻接矩阵实现的广度优先搜索算法 void BFS(MGraph G, int i) { visit(i); // 对i号结点访问 Visited[i] = true; // 标记i号结点已访问 EnQueue(Q, i); // 将i号结点入队 while(!QueueEmpty(Q)) { DeQueue(Q, v); // 队头结点出队 for(int j = 0; j < G.vexnum; j++) { // 遍历v的邻接矩阵 if(G.Edge[v][j] && !Visited[j]) { // 如果存在边且邻接点未访问 visit(j); // 访问邻接点 Visited[j] = true; // 标记邻接点已访问 EnQueue(Q, j); // 将邻接点入队 } } } }对于⽆向图,调⽤BFS函数的次数=连通分量数复杂度分析 空间复杂度:最坏情况,辅助队列⼤⼩为 $O(|V|)$ 时间复杂度: 邻接矩阵需要访问V个顶点,V个顶点又要访问V个顶点,所以时间复杂度为 $O(|V|^2)$,邻接表访问V个顶点,每个顶点访问其边表,边表的总长度为$|E|$,所以时间复杂度为 $O(|V| + |E|)$。 BFS算法求解单源最短路径问题 如果是一个不带权的图,广度优先搜索可以用来求解单源最短路径问题。广度优先搜索的每次访问都是从当前顶点到其邻接顶点的距离为1,因为广度优先搜索总是按照距离由近至远来遍历图中每个顶点的。具体代码示例如下: void BFS_ShortestPath(MGraph G, int u) { //d[i]表示从u到i的最短距离 for(int i = 0; i < G.vexnum; i++) { d[i] = INFINITY; // 初始化距离为无穷大 Visited[i] = false; // 初始化访问标记 path[i] = -1;//这里引入一个path数组,记录从起点到i的路径 } d[u] = 0; // 起点到自身的距离为0 EnQueue(Q, u); // 将起点入队 Visited[u] = true; // 标记起点已访问 while(!QueueEmpty(Q)) { DeQueue(Q, v); // 队头结点出队 for(w=FirstNeighbor(G,v); w!=-1; w=NextNeighbor(G,v,w)) { if(!Visited[w]) { // 如果邻接点未访问 Visited[w] = true; // 标记邻接点已访问 d[w] = d[v] + 1; // 更新距离 path[w] = v; // 记录路径 EnQueue(Q, w); // 将邻接点入队 } } } }广度优先生成树 在广度遍历的过程中,广度优先遍历的过程中,生成的树就是广度优先生成树。⼴度优先⽣成树由⼴度优先遍历过程确定。由于一定的图邻接矩阵表示法是唯一的,其广度优先生成树也是唯一的,但由于邻接表存储一个图不是唯一的,故其广度优先生成树也不是唯一的。 对⾮连通图的⼴度优先遍历,可得到⼴度优先⽣成森林 深度优先搜索 深度优先搜索(DFS,Depth-First Search)会优先考虑最后被发现的顶点,也就是说离起点越远的顶点其优先级越高。 对于同一个图,基于邻接矩阵的遍历所得到的DFS序列和BFS序列是唯一的。基于邻接表的遍历所得到的DFS序列和BFS序列不是唯一的。基本思想 类似于树的先序遍历。首先访问图中某一起始顶点v,然后由v出发,访问于v邻接且未被访问的任一顶点$w_1$,再访问与$w_1$邻接且未被访问的任一顶点$w_2$,重复上述过程。 代码实现 bool Visited[MAX_VERTEX_NUM]; // 访问标记数组 void DFSTraverse(Graph G) { for(int i = 0; i < G.vexnum; i++){ Visited[i] = false; // 初始化访问标记数组 } for(int i = 0; i < G.vexnum; i++){ //这里为了保证此图如果是一个非连通图,也能达成目的 if(!Visited[i]){ DFS(G, i); } } } //用邻接表实现的深度优先搜索算法 void DFS(ALGraph G, int i) { visit(i); // 对i号结点访问 Visited[i] = true; // 标记i号结点已访问 for(p=G.vertices[i].first; p!=NULL; p=p->next) { // 遍历i的边表 w=p->adjvex; // 获取邻接点 if(!Visited[w]) { // 如果邻接点未访问 DFS(G, w); // 递归访问邻接点 } } } //使用邻接矩阵实现的深度优先搜索算法 void DFS(MGraph G, int i) { visit(i); // 对i号结点访问 Visited[i] = true; // 标记i号结点已访问 for(int j = 0; j < G.vexnum; j++) { // 遍历i的邻接矩阵 if(G.Edge[i][j] && !Visited[j]) { // 如果存在边且邻接点未访问 DFS(G, j); // 递归访问邻接点 } } }复杂度分析 DFS是一个递归算法,需要一个递归工作栈,故空间复杂度$O(|V|)$ 时间复杂度和BFS类似,邻接矩阵$O(|V|^2)$,邻接表$O(|V| + |E|)$。 深度优先生成树 深度优先搜索也会产生一颗深度优先生成树,和BFS类似。 对⾮连通图的深度优先遍历,可得到深度优先生成森林。 图的遍历与图的连通性 对于无向图,调用BFS和DFS的次数等于它的连通分量数量。 有向图,非强连通分量调用一次BFS或DFS无法访问到该连通分量的所有顶点。 图的应用 最小生成树 连通图的生成树是包含图中全部顶点的一个极小连通子图。若生成树的边的权值之和最小,则称为最小生成树。 官方定义:对于⼀个带权连通⽆向图G = (V, E),⽣成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有⽣成树的集合,若T为R中边的权值之和最⼩的⽣成树,则T称为G的最⼩⽣成树(Minimum-Spanning-Tree, MST)。 其性质如下: 不是唯一的.当图G中的各边权值不等时,是唯一的. 最小生成树的边的权值之和总是唯一的.而且是最小的 边数=顶点数-1 只有连通图才有⽣成树,⾮连通图只有⽣成森林 如果⼀个连通图本身就是⼀棵树,则其最⼩⽣成树就是它本身 也有两种方法求解最小生成树,分别是Prim算法和Kruskal算法。 Prim算法 从某⼀个顶点开始构建⽣成树;每次将代价最⼩的新顶点纳⼊⽣成树,直到所有顶点都纳⼊为⽌。 算法步骤如图所示: Prim算法示意图图片 Kruskal算法 每次选择⼀条权值最⼩的边,使这条边的两头连通(原本已经连通的就不选)直到所有结点都连通。 算法步骤如图所示: Kruskal算法示意图图片 Prim算法和Kruskal算法的对比 属性Prim算法Kruskal算法基本思想从某一顶点开始,逐步扩展生成树从边的集合开始,逐步选择边加入生成树适用场景稠密图稀疏图时间复杂度$O(\vert V \vert^2)$$O(\vert E \vert \log \vert E \vert)$Kruskal算法通常用堆来存储边的集合。最短路径问题 BFS求解单源最短路径问题 详见:[[#BFS算法求解单源最短路径问题]] Dijkstra算法单源最短路径算法 [[#^Cite1|带权路径长度]]:当图是带权图时,⼀条路径上所有边的权值之和,称为该路径的带权路径⻓度。 BFS算法适用于不带权图(或等权图)的单源最短路径问题,而Dijkstra算法适用于带权图的单源最短路径问题。 Dijkstra算法:三个辅助数组:dist[],记录由源点$v_0$到各顶点当前的最短长度;path[]表示从源点到顶点i之间的最短路径的前驱结点,final[]表示顶点i是否已经找到最短路径。 过程如下所示: Dijkstra算法过程图片 注意:Dijkstra算法不能用于带有负权边的图。 时间复杂度:$O(|V|^2)$ Floyd算法求解个各顶点间的最短路径 Floyd算法:求出每⼀对顶点之间的最短路径。 对于每一对顶点 $i$ 和 $j$,以及中间顶点 $k$,有如下递推关系:若 $A^{(k-1)}[i][j] > A^{(k-1)}[i][k] + A^{(k-1)}[k][j]$,则更新 $A^{(k)}[i][j]$ 和 $path^{(k)}[i][j]$,否则保持原值。 算法执行过程如下图所示: Floyd算法执行过程图片 注意:Floyd可以用于负权图,Floyd 算法不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径BFS、Dijkstra和Floyd算法的对比 特性BFS 算法Dijkstra 算法Floyd 算法无权图✓✓✓带权图✗✓✓带负权值的图✗✗✓带负权回路的图✗✗✗时间复杂度$( O(\vert V\vert^2) )$ 或 $( O(\vert V\vert + \vert E\vert) )$$( O(\vert V\vert^2) )$$( O(\vert V\vert^3) )$通常用于求无权图的单源最短路径求带权图的单源最短路径求带权图中各顶点间的最短路径Dijkstra应说的话也可以求各个顶点间的最短路径,就是每个顶点执行一次Dijkstra算法,时间复杂度就是$( O(\vert V\vert^3) )$有向无环图描述表达式 有向⽆环图:若⼀个有向图中不存在环,则称为有向⽆环图,简称DAG图(Directed Acyclic Graph) 如下图是$((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e)$的二叉树表示和有向无环图表示 有向无环图描述表达式示意图图片 拓扑排序 AOV网(Activity On Vertex Network,顶点表示活动的网络):用有向无环图(DAG)来表示一个工程。顶点表示活动,有向边 $\langle V_i, V_j \rangle$ 表示活动 $V_i$ 必须先于活动 $V_j$ 进行。 拓扑排序:在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序: 每个顶点出现且只出现一次。 若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径。 或定义为:拓扑排序是对有向无环图的顶点的一种排序,它使得若存在一条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。 拓扑排序的算法步骤如下: 从DAG图中选择一个没有前驱的顶点并输出 从图中删除该顶点和所有以它为起点的边 重复上述过程直到当前为空或不存在无前驱的顶点(有环)为止 如下图是一个拓扑排序的例子: 拓扑排序示例图片 如下是基于邻接表的拓扑排序实现: void TopologicalSort(ALGraph G) { InitStack(S); for (int i = 0; i < G.vexnum; i++) { if (G.vexs[i].in == 0) {// 如果顶点的入度为0 Push(S, i); // 将顶点入栈 } } int count = 0; // 计数器,记录已输出的顶点数 while (!StackEmpty(S)) { Pop(S, v); // 栈顶元素出栈 printf("%c ", G.vexs[v].data); // 输出顶点 count++;// 已输出顶点数加1 for(p=G.vexs[v].first;p!=NULL;p=p->next){ //将所有v指向的顶点的入度减1 w = p->adjvex; // 获取邻接点 if(--G.vexs[w].in==0) { // 如果入度减为0 Push(S, w); // 将入度为0的顶点入栈 } } } if(count<G.vexnum) { printf("图中存在环,无法进行拓扑排序。\n"); } else { printf("\n拓扑排序完成。\n"); } } 时间复杂度:$O(|V| + |E|)$(邻接表实现),$O(|V|^2)$(邻接矩阵实现) 排序结果不唯一 工程可以从入度为0的顶点开始(不存在前驱) 对于一般的图来说,其邻接矩阵是三角矩阵,则存在拓扑排序;反之不一定成立。 逆拓扑排序:拓扑排序的逆序称为逆拓扑排序。具体过程就是把出度为0的顶点输出,删除该点和以该点为终点的有向边。关键路径 在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为⽤边表示活动的⽹络,简称AOE⽹ (Activity On Edge NetWork) AOE⽹具有以下两个性质: 只有在某顶点所代表的事件发⽣后,从该顶点出发的各有向边所代表的活动才能开始; 只有在进⼊某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发⽣。另外,有些活动是可以并⾏进⾏的 在AOE⽹中仅有⼀个 ⼊度 为0的顶点,称为开始顶点(源点),它表示整个⼯程的开始。也仅有⼀个出度为0的顶点,称为结束顶点(汇点),它表示整个⼯程的结束。 从源点到汇点的有向路径可能有多条,所有路径中,具有最⼤路径⻓度的路径称为关键路径,⽽把关键路径上的活动称为关键活动,完成整个⼯程的最短时间就是关键路径的⻓度,若关键活动不能按时完成,则整个⼯程的完成时间就会延⻓。 以下是几种参考的量的定义: 事件 $v_k$ 的最早发生时间 $v_e(k)$ 指从开始顶点 $V$ 到事件 $v_k$ 的最长路径长度。计算公式为: $$ v_e(k) = \max \{ v_e(j) + \text{Weight}(v_j, v_k) \} $$其中 $\text{Weight}(v_j, v_k)$ 表示边 $\langle v_j, v_k \rangle$ 的权值。$v_e(k)$ 按从前往后的顺序计算。 事件 $v_k$ 的最迟发生时间 $v_l(k)$ 指在不推迟整个工程完成的前提下,事件 $v_k$ 最迟必须发生的时间。计算公式为: $$ v_l(j) = \min \{ v_l(k) - \text{Weight}(v_j, v_k) \} $$其中 $\text{Weight}(v_j, v_k)$ 表示边 $\langle v_j, v_k \rangle$ 的权值。$v_l(j)$ 按从后往前的顺序计算。 活动 $a_i$ 的最早开始时间 $e(i)$ 即该活动的起点事件的最早发生时间。若边 $\langle v_k, v_j \rangle$ 表示活动 $a_i$,则 $$ e(i) = v_e(k) $$ 活动 $a_i$ 的最迟开始时间 $l(i)$ 即活动终点事件的最迟发生时间减去该活动所需时间。若边 $\langle v_k, v_j \rangle$ 表示活动 $a_i$,则 $$ l(i) = v_l(j) - \text{Weight}(v_k, v_j) $$ 活动 $a_i$ 的时间余量 $d(i)$ 即最迟开始时间与最早开始时间之差: $$ d(i) = l(i) - e(i) $$$d(i)$ 表示在不增加整个工程完成时间的前提下,活动 $a_i$ 可以拖延的最大时间。若 $d(i) = 0$,则该活动为关键活动,必须如期完成。 求关键路径的算法: 求所有$v_e()$ 求所有$v_l()$ 求所有e() 求所有l() 求所有d(),找出关键路径 d(k)=0的活动就是关键活动, 由关键活动可得关键路径 如下图所示是一个求解关键路径的示例: 求解关键路径示例图片 注意以下几点: 关键路径所有活动都是关键活动 关键路径不唯一 加速某一关键活动不一定缩短整个工程的工期.因为AOE网中存在多条关键路径.可能存在称为"桥"的一种特殊关键活动,它位于所有的关键路径上,只有它加速才会缩短整个工期。 番外篇:采用不同存储结构时各种图算法的时间复杂度 存储结构DijkstraFloydPrimKruskalDFSBFS拓扑排序关键路径邻接矩阵$O(n^2)$$O(n^3)$$O(n^2)$-$O(n^2)$$O(n^2)$$O(n^2)$$O(n^2)$邻接表---$O(e\log _2 e)$$O(n+e)$$O(n+e)$$O(n+e)$$O(n+e)$
【计算机考研(408)- 数据结构】图 图 图的定义 图 $G$ 由顶点集 $V$ 和边集 $E$ 组成,记为 $G = (V, E)$,其中 $V(G)$ 表示图 $G$ 中顶点的有限非空集,$E(G)$ 表示图 $G$ 中顶点之间的关系(边)集合。若 $V = \{v_1, v_2, \ldots, v_n\}$,则用 $|V|$ 表示图 $G$ 中顶点的个数(称为图的阶),$E = \{(u, v) \mid u \in V, v \in V\}$,用 $|E|$ 表示图 $G$ 中边的条数。 线性表可以是空表,树可以是空树,但是图不能是空图,即使他没有边,他也不能没有顶点,也就是说图中不能一个定点都没有,但边集E可以为空。 G:Graph V:Vertex E:Edge来点题外话:假设南昌东站、昌北机场站、共青城东站、庐山东站是一个个顶点V,那么连接他们之间的铁路可以看作是边E,那么构成的图G就是一张图。也就是京港高铁昌九段,在延申一点就是全国高铁网络均可看作是一张大图。 有关图的相关概念 有向图和无向图 有向图:若 $E$ 是有向边(弧)的有限集合,则图 $G$ 为有向图。弧是顶点的有序对,记为 $\langle v, w \rangle$,其中 $v$、$w$ 是顶点,$v$ 称为弧尾,$w$ 称为弧头,$\langle v, w \rangle$ 表示从顶点 $v$ 到顶点 $w$ 的弧。$\langle v, w \rangle \ne \langle w, v \rangle$。 无向图:若 $E$ 是无向边(边)的有限集合,则图 $G$ 为无向图。无向边是顶点的无序对,记为 $(v, w)$ 或 $(w, v)$,其中 $v$、$w$ 是顶点,且 $(v, w) = (w, v)$。 示例: 有向图 $G_1 = (V_1, E_1)$ $V_1 = \{A, B, C, D, E\}$ $E_1 = \{\langle A, B \rangle, \langle A, C \rangle, \langle A, D \rangle, \langle A, E \rangle, \langle B, A \rangle, \langle B, C \rangle, \langle B, E \rangle, \langle C, D \rangle\}$ 无向图 $G_2 = (V_2, E_2)$ $V_2 = \{A, B, C, D, E\}$ $E_2 = \{(A, B), (B, D), (B, E), (C, D), (C, E), (D, E)\}$ 有向图无向图示例图片 简单图和多重图 简单图:满足不存在重复边,不存在顶点到自身的边。数据结构只讨论简单图。 多重图:两个结点的边数多余一条,且允许有顶点到自身的边。与简单图相对。 简单图/多重图图片 顶点的度 无向图 顶点的度:一个顶点的度等于依附于该顶点的边的条数。记作$TD(v)$ 所有顶点的度之和等于边数的两倍。 在具有n个顶点,e条边的无向图图,$\sum^n_{i=1}TD(v_i)=2e$ 有向图 入度:以该顶点为终点的有向边的条数。记作$ID(v)$ 出度:以该顶点为起点的有向边的条数。记作$OD(v)$ 顶点的度 = 入度 + 出度。$TD(v)=ID(v)+OD(v)$ 所有顶点的入度之和等于所有顶点的出度之和,且都等于边的总数。 在具有n个顶点,e条边的有向图,$\sum^n_{i=1}ID(v_i)=\sum^n_{i=1}OD(v_i)=e$ 顶点之间的关系的描述 路径:顶点 $v_p$ 到顶点 $v_q$ 之间的一条路径是指顶点序列,$v_p, v_{i_1}, v_{i_2}, \ldots, v_{i_m}, v_q$ 。 回路:第一个顶点和最后一个顶点相同的路径称为回路或环。$v_p, v_{i_1}, v_{i_2}, \ldots, v_{i_m}, v_p$ 。 简单路径:在路径序列中,顶点不重复出现的路径称为简单路径。 简单回路:除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。 路径长度:路径上边的数目。 点到点的距离:从顶点 $u$ 出发到顶点 $v$ 的最短路径(若存在),此路径的长度称为从 $u$ 到 $v$ 的距离。若从 $u$ 到 $v$ 根本不存在路径,则记该距离为无穷($\infty$)。 若一个图有n个顶点,且边数大于n-1,则此图一定有环。 在有向图中,如果从顶点v到顶点w和从顶点w到顶点v都有路径,则称这两个顶点是强连通的。 在无向图中,如果从顶点v到顶点w有路径存在,则称这两个顶点是连通的。 图的连通性(连通图、强连通图) 连通图:若图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。 对于有 $n$ 个顶点的无向图 $G$,若 $G$ 是连通图,则最少有 $n-1$ 条边。若 $G$ 是非连通图,则最多可能有$C_{n-1}^2$条边。 强连通图:若图中任何一对顶点都是强连通的,则称此图为强连通图。 对于有 $n$ 个顶点的有向图 $G$,若 $G$ 是强连通图,则最少有$n$条边(形成回路)。 连通分量:无向图中的极大连通子图([[#子图]]必须连通,且包含尽可能多的顶点和边)称为连通分量。 说句题外的例子:如果我们把刚刚拓展到全国铁路网看作是一张图G,那么相应的京港高速铁路昌九段就是一个子图,那么相应的,大陆地区/台湾地区/海南省的铁路网就是这张图的连通分量。 强连通分量:有向图 $G$ 中的极大强连通子图([[#子图]]必须强连通,且包含尽可能多的顶点和边)称为强连通分量。 子图 子图:设有两个图 $G = (V, E)$ 和 $G' = (V', E')$,若 $V' \subseteq V$ 且 $E' \subseteq E$,则称 $G'$ 是 $G$ 的子图。若 $V(G') = V(G)$,则称 $G'$ 为 $G$ 的生成子图(即包含全部顶点的子图)。 生成树&生成森林 连通图的生成树是包含全部顶点的极小连通子图(边要尽可能地少,但要保持连通)。若顶点为n,则有n-1条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。 在非连通图中,连通分量的生成树构成非连通图的生成森林。 边的权、带权图 边的权:在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。 带权图(网):边上带有权值的图称为带权图,也称网。 带权路径长度:当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度。 ^Cite1 还是上面的例子,如果我们在每个边上表明两个车站之间的距离,那么这个图就是带权图。 几种特殊的图 无向完全图:无向图中任意两个顶点之间都存在边。 若无向图的顶点数 $|V| = n$,则边的数目 $|E|$ 的取值范围为 $0 \leq |E| \leq \frac{n(n-1)}{2}$ 。(即$C_n^2$) 有向完全图:有向图中任意两个顶点之间都存在方向相反的两条弧。 若有向图的顶点数$|V|=n$,则弧的数目 $|E|$ 的取值范围为 $0 \leq |E| \leq n(n-1)$ 。(即$2C_n^2$) 稀疏图:边数很少的图。反之称为稠密图。 注意,以上没有一个绝对的界限,一般来说$|E| < |V|log|V|$时,可以将G视为稀疏图 有向树:一个顶点的入度为0、其余顶点的入度为1的有向图,称为有向树。 树,不存在回路且连通的无向图,n个顶点的树有n-1条边。图的存储 邻接矩阵法 定义 邻接矩阵是指用一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息(各顶点间的邻接关系),存储顶点之间邻接关系的二维数组称为邻接矩阵。 结点数为$n$的图$G = (V, E)$的邻接矩阵A是$n*n$的。将G的顶点编号为$v_1, v_2, \ldots, v_n$,则: $$ A[i][j] = \begin{cases} 1, & \text{若}(v_i, v_j)\text{或}<v_i,v_j>\text{是E(G)中的边} \\ 0, & \text{若}(v_i, v_j)\text{或}<v_i,v_j>\text{不是E(G)中的边} \end{cases} $$以下是图的邻接矩阵示意图: 图的邻接矩阵示例图片 以下是带权图(网的)的邻接矩阵示意图: 带权图的邻接矩阵示例图片 对角线元素也经常用0表示代码实现 //图的邻接矩阵 #define MaxVertexNum 100 // 顶点数目的最大值 typedef struct{ char Vex[MaxVertexNum];//顶点表(这里可以拓展,存更多的信息) int Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵(当然也可以是bool型) int vexnum,edgenum;//顶点数和边数 }MGraph;//带权图的邻接矩阵(同时也对其进行了一定的拓展) #define MaxVertexNum 100 // 顶点数目的最大值 #define INFINITY MAX_INT //无穷大 typedef char VertexType;//顶点类型 tyepedef int EdgeType;//边的权值类型 typedef struct{ VertexType Vex[MaxVertexNum];//顶点表(这里可以拓展,存更多的信息) EdgeType Edge[MaxVertexNum][MaxVertexNum];//这里需要存储边的权值 int vexnum,edgenum;//顶点数和边数 }MGraph;特点 对无向图,第i个结点的度$TD(i)$=第i行(或第i列)非零元素的个数 对有向图,第i个结点的入度$ID(i)$=第i行非零元素(或非∞元素)的个数 对有向图,第i个结点的出度$OD(i)$=第i列非零元素(或非∞元素)的个数 第i个结点的度=第i行、第i列的非零元素个数之和 对于无向图的邻接矩阵一定是一个[[数组和特殊矩阵#对称矩阵]],所以在实际存储邻接矩阵的时候只需要存储上(或下)三角矩阵的元素。 稠密图适合用此方法表示。 设图G的邻接矩阵为A(矩阵元素为0/1),则$A^n$的元素$A^n[i][j]$等于由顶点i到顶点j的长度为n的路径的数目。 复杂度分析 空间复杂度:$O(|V|^2)$ ,其只和顶点数相关,和实际的边数无关 邻接矩阵法求顶点的度/出度/入度的时间复杂度:$O(|V|)$ 适合用于存储稠密图 无向图的邻接矩阵是对称矩阵,可以压缩存储(只存储上三角区/下三角区) 邻接表法 定义 邻接表,对图G中的每个顶点$v_i$建立一个单链表,第i个单链表中的结点表示依附于顶点$v_i$的边(对于有向图而言则是以顶点$v_i$为尾的弧,假设1->2,则挂在1上),这个单链表就是顶点$v_i$的边表(有向图中叫做出边表)。边表的头指针和顶点的数据信息采用顺序存储,称为顶点表,所以在邻接表中存在两种结点,顶点表结点和边表结点。 如下图所示,即为顶点表和边表的结点结构 顶点表和边表的数据结构图片 顶点表结点由顶点信息(存储顶点相关信息)和边表头指针(指向第一条边的边表结点)组成,边表结点由邻接点域(存储头结点顶点邻接的顶点编号)和指针域(指向下一条的边表结点)组成。 如图所示是有向图和无向图邻接表表示法的示例: 有向图和无向图邻接表表示法示例图片 代码实现 #define MaxVertexNum 100 // 最大顶点数 typedef struct ArcNode{ //边表结点 int adjvex; // 该弧指向的顶点的位置 struct ArcNode *next; // 指向下一条边的指针 // 其他信息(如权值等)可以在此处添加 } ArcNode; typedef struct VNode{ //顶点表结点 VertexType data; // 顶点信息 ArcNode *first; // 指向第一条弧的指针 } VNode,AdjList[MaxVertexNum]; typedef struct{ AdjList vertices; //邻接表 int vexnum,arcnum; //顶点数和弧数 } ALGraph;特点 适用于稀疏图 表示不唯一 复杂度分析 空间复杂度:$O(|V| + |E|)$(有向图),$O(|V| + 2|E|)$(无向图),其和顶点数、边数相关。 对于稀疏图,邻接表法比邻接矩阵法更节省空间。 十字链表法 十字链表是有向图的一种存储结构,十字链表中,每个弧有个结点,每个顶点也有一个结点。 下面是一个弧节点和顶点结点的示意图: 弧节点和顶点结点的示意图图片 以下是一个十字链表存储有向图的示意图: 十字链表存储有向图的示意图图片 空间复杂度:$O(|V| + |E|)$ 沿着绿色线路则是出边 沿着橙色线路则是入边 只能存储有向图 十字链表表示是不唯一的,但是一个十字链表表示唯一确定的一个图。 邻接多重表 邻接多重表是无向图的一种链式存储结构。与十字链表类似的是其边也用一个结点表示, 下面是一个邻接多重表的边节点和顶点结点的示意图: 邻接多重表的边节点和顶点结点的示意图图片 以下是一个邻接多重表存储无向图的示意图: 邻接多重表存储无向图的示意图图片 空间复杂度:$O(|V| + |E|)$ 只存储无向图 图的存储四种方法对比 属性邻接矩阵邻接表十字链表邻接多重表空间复杂度$O(\vert V\vert^2)$无向图 $O(\vert V\vert + 2\vert E\vert)$,有向图 $O(\vert V\vert + \vert E\vert)$$O(\vert V\vert + \vert E\vert)$$O(\vert V\vert + \vert E\vert)$找相邻边遍历对应行或列时间复杂度为$O(\vert V\vert)$找有向图的入边必须遍历整个邻接表很方便很方便删除边或顶点删除边很方便,删除顶点需要大量移动数据无向图中删除边或顶点都不方便很方便很方便适用于稠密图稀疏图和其他只能存有向图只能存无向图表示方式唯一不唯一不唯一不唯一图的基本操作 Adjacent(G, x, y) 判断图 $G$ 是否存在边 $\langle x, y \rangle$ 或 $(x, y)$。 Neighbors(G, x) 列出图 $G$ 中与结点 $x$ 邻接的所有顶点。 InsertVertex(G, x) 在图 $G$ 中插入顶点 $x$。 DeleteVertex(G, x) 从图 $G$ 中删除顶点 $x$ 及其相关的所有边。 AddEdge(G, x, y) 若无向边 $(x, y)$ 或有向边 $\langle x, y \rangle$ 不存在,则向图 $G$ 中添加该边。 RemoveEdge(G, x, y) 若无向边 $(x, y)$ 或有向边 $\langle x, y \rangle$ 存在,则从图 $G$ 中删除该边。 FirstNeighbor(G, x) 求图 $G$ 中顶点 $x$ 的第一个邻接点,若有则返回顶点号;若 $x$ 没有邻接点或图中不存在 $x$,则返回 $-1$。 NextNeighbor(G, x, y) 假设图 $G$ 中顶点 $y$ 是顶点 $x$ 的一个邻接点,返回除 $y$ 之外顶点 $x$ 的下一个邻接点的顶点号;若 $y$ 是 $x$ 的最后一个邻接点,则返回 $-1$。 Get_edge_value(G, x, y) 获取图 $G$ 中边 $(x, y)$ 或 $\langle x, y \rangle$ 对应的权值。 Set_edge_value(G, x, y, v) 设置图 $G$ 中边 $(x, y)$ 或 $\langle x, y \rangle$ 的权值为 $v$。 除此之外,还有[[#图的遍历|图的遍历]]相关操作。 图的遍历 广度优先搜索 广度优先搜索(BFS,Breadth-First Search)会优先考虑最早被发现的顶点,也就是说离起点越近的顶点其优先级越高。 基本思想 类似于二叉树的层序遍历。基本思想是:首先访问起始顶点v,接着由v出发,依次访问v的各个未访问过的邻接顶点$w_1,w_2,...,w_i$,然后依次访问$w_1,w_2,...,w_i$的所有未被访问过的邻接顶点;再从这些访问过的顶点出发,访问它们所有未被访问过的邻接顶点……。 为了实现逐层访问,必须借助一个辅助队列,用来记忆正在访问的顶点的下一层顶点。 代码实现 bool Visited[MAX_VERTEX_NUM]; // 访问标记数组 void BFSTraverse(Graph G) { for(int i = 0; i < G.vexnum; i++){ Visited[i] = false; // 初始化访问标记数组 } InitQueue(Q); for(int i = 0; i < G.vexnum; i++){//这里为了保证此图如果是一个非连通图,也能达成目的 if(!Visited[i]){ BFS(G, i); } } } //用邻接表实现的广度优先搜索算法 void BFS(ALGraph G, int i) { visit(i);//对i号结点访问 Visited[i] = true; // 标记i号结点已访问 EnQueue(Q, i); // 将i号结点入队 while(!QueueEmpty(Q)) { DeQueue(Q, v); // 队头结点出队 for(p=G.vertices[v].first; p!=NULL;p=p->next){// 遍历v的边表 w=p->adjvex; // 获取邻接点 if(!Visited[w]){ // 如果邻接点未访问 visit(w); // 访问邻接点 Visited[w] = true; // 标记邻接点已访问 EnQueue(Q, w); // 将邻接点入队 } } } } //使用邻接矩阵实现的广度优先搜索算法 void BFS(MGraph G, int i) { visit(i); // 对i号结点访问 Visited[i] = true; // 标记i号结点已访问 EnQueue(Q, i); // 将i号结点入队 while(!QueueEmpty(Q)) { DeQueue(Q, v); // 队头结点出队 for(int j = 0; j < G.vexnum; j++) { // 遍历v的邻接矩阵 if(G.Edge[v][j] && !Visited[j]) { // 如果存在边且邻接点未访问 visit(j); // 访问邻接点 Visited[j] = true; // 标记邻接点已访问 EnQueue(Q, j); // 将邻接点入队 } } } }对于⽆向图,调⽤BFS函数的次数=连通分量数复杂度分析 空间复杂度:最坏情况,辅助队列⼤⼩为 $O(|V|)$ 时间复杂度: 邻接矩阵需要访问V个顶点,V个顶点又要访问V个顶点,所以时间复杂度为 $O(|V|^2)$,邻接表访问V个顶点,每个顶点访问其边表,边表的总长度为$|E|$,所以时间复杂度为 $O(|V| + |E|)$。 BFS算法求解单源最短路径问题 如果是一个不带权的图,广度优先搜索可以用来求解单源最短路径问题。广度优先搜索的每次访问都是从当前顶点到其邻接顶点的距离为1,因为广度优先搜索总是按照距离由近至远来遍历图中每个顶点的。具体代码示例如下: void BFS_ShortestPath(MGraph G, int u) { //d[i]表示从u到i的最短距离 for(int i = 0; i < G.vexnum; i++) { d[i] = INFINITY; // 初始化距离为无穷大 Visited[i] = false; // 初始化访问标记 path[i] = -1;//这里引入一个path数组,记录从起点到i的路径 } d[u] = 0; // 起点到自身的距离为0 EnQueue(Q, u); // 将起点入队 Visited[u] = true; // 标记起点已访问 while(!QueueEmpty(Q)) { DeQueue(Q, v); // 队头结点出队 for(w=FirstNeighbor(G,v); w!=-1; w=NextNeighbor(G,v,w)) { if(!Visited[w]) { // 如果邻接点未访问 Visited[w] = true; // 标记邻接点已访问 d[w] = d[v] + 1; // 更新距离 path[w] = v; // 记录路径 EnQueue(Q, w); // 将邻接点入队 } } } }广度优先生成树 在广度遍历的过程中,广度优先遍历的过程中,生成的树就是广度优先生成树。⼴度优先⽣成树由⼴度优先遍历过程确定。由于一定的图邻接矩阵表示法是唯一的,其广度优先生成树也是唯一的,但由于邻接表存储一个图不是唯一的,故其广度优先生成树也不是唯一的。 对⾮连通图的⼴度优先遍历,可得到⼴度优先⽣成森林 深度优先搜索 深度优先搜索(DFS,Depth-First Search)会优先考虑最后被发现的顶点,也就是说离起点越远的顶点其优先级越高。 对于同一个图,基于邻接矩阵的遍历所得到的DFS序列和BFS序列是唯一的。基于邻接表的遍历所得到的DFS序列和BFS序列不是唯一的。基本思想 类似于树的先序遍历。首先访问图中某一起始顶点v,然后由v出发,访问于v邻接且未被访问的任一顶点$w_1$,再访问与$w_1$邻接且未被访问的任一顶点$w_2$,重复上述过程。 代码实现 bool Visited[MAX_VERTEX_NUM]; // 访问标记数组 void DFSTraverse(Graph G) { for(int i = 0; i < G.vexnum; i++){ Visited[i] = false; // 初始化访问标记数组 } for(int i = 0; i < G.vexnum; i++){ //这里为了保证此图如果是一个非连通图,也能达成目的 if(!Visited[i]){ DFS(G, i); } } } //用邻接表实现的深度优先搜索算法 void DFS(ALGraph G, int i) { visit(i); // 对i号结点访问 Visited[i] = true; // 标记i号结点已访问 for(p=G.vertices[i].first; p!=NULL; p=p->next) { // 遍历i的边表 w=p->adjvex; // 获取邻接点 if(!Visited[w]) { // 如果邻接点未访问 DFS(G, w); // 递归访问邻接点 } } } //使用邻接矩阵实现的深度优先搜索算法 void DFS(MGraph G, int i) { visit(i); // 对i号结点访问 Visited[i] = true; // 标记i号结点已访问 for(int j = 0; j < G.vexnum; j++) { // 遍历i的邻接矩阵 if(G.Edge[i][j] && !Visited[j]) { // 如果存在边且邻接点未访问 DFS(G, j); // 递归访问邻接点 } } }复杂度分析 DFS是一个递归算法,需要一个递归工作栈,故空间复杂度$O(|V|)$ 时间复杂度和BFS类似,邻接矩阵$O(|V|^2)$,邻接表$O(|V| + |E|)$。 深度优先生成树 深度优先搜索也会产生一颗深度优先生成树,和BFS类似。 对⾮连通图的深度优先遍历,可得到深度优先生成森林。 图的遍历与图的连通性 对于无向图,调用BFS和DFS的次数等于它的连通分量数量。 有向图,非强连通分量调用一次BFS或DFS无法访问到该连通分量的所有顶点。 图的应用 最小生成树 连通图的生成树是包含图中全部顶点的一个极小连通子图。若生成树的边的权值之和最小,则称为最小生成树。 官方定义:对于⼀个带权连通⽆向图G = (V, E),⽣成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有⽣成树的集合,若T为R中边的权值之和最⼩的⽣成树,则T称为G的最⼩⽣成树(Minimum-Spanning-Tree, MST)。 其性质如下: 不是唯一的.当图G中的各边权值不等时,是唯一的. 最小生成树的边的权值之和总是唯一的.而且是最小的 边数=顶点数-1 只有连通图才有⽣成树,⾮连通图只有⽣成森林 如果⼀个连通图本身就是⼀棵树,则其最⼩⽣成树就是它本身 也有两种方法求解最小生成树,分别是Prim算法和Kruskal算法。 Prim算法 从某⼀个顶点开始构建⽣成树;每次将代价最⼩的新顶点纳⼊⽣成树,直到所有顶点都纳⼊为⽌。 算法步骤如图所示: Prim算法示意图图片 Kruskal算法 每次选择⼀条权值最⼩的边,使这条边的两头连通(原本已经连通的就不选)直到所有结点都连通。 算法步骤如图所示: Kruskal算法示意图图片 Prim算法和Kruskal算法的对比 属性Prim算法Kruskal算法基本思想从某一顶点开始,逐步扩展生成树从边的集合开始,逐步选择边加入生成树适用场景稠密图稀疏图时间复杂度$O(\vert V \vert^2)$$O(\vert E \vert \log \vert E \vert)$Kruskal算法通常用堆来存储边的集合。最短路径问题 BFS求解单源最短路径问题 详见:[[#BFS算法求解单源最短路径问题]] Dijkstra算法单源最短路径算法 [[#^Cite1|带权路径长度]]:当图是带权图时,⼀条路径上所有边的权值之和,称为该路径的带权路径⻓度。 BFS算法适用于不带权图(或等权图)的单源最短路径问题,而Dijkstra算法适用于带权图的单源最短路径问题。 Dijkstra算法:三个辅助数组:dist[],记录由源点$v_0$到各顶点当前的最短长度;path[]表示从源点到顶点i之间的最短路径的前驱结点,final[]表示顶点i是否已经找到最短路径。 过程如下所示: Dijkstra算法过程图片 注意:Dijkstra算法不能用于带有负权边的图。 时间复杂度:$O(|V|^2)$ Floyd算法求解个各顶点间的最短路径 Floyd算法:求出每⼀对顶点之间的最短路径。 对于每一对顶点 $i$ 和 $j$,以及中间顶点 $k$,有如下递推关系:若 $A^{(k-1)}[i][j] > A^{(k-1)}[i][k] + A^{(k-1)}[k][j]$,则更新 $A^{(k)}[i][j]$ 和 $path^{(k)}[i][j]$,否则保持原值。 算法执行过程如下图所示: Floyd算法执行过程图片 注意:Floyd可以用于负权图,Floyd 算法不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径BFS、Dijkstra和Floyd算法的对比 特性BFS 算法Dijkstra 算法Floyd 算法无权图✓✓✓带权图✗✓✓带负权值的图✗✗✓带负权回路的图✗✗✗时间复杂度$( O(\vert V\vert^2) )$ 或 $( O(\vert V\vert + \vert E\vert) )$$( O(\vert V\vert^2) )$$( O(\vert V\vert^3) )$通常用于求无权图的单源最短路径求带权图的单源最短路径求带权图中各顶点间的最短路径Dijkstra应说的话也可以求各个顶点间的最短路径,就是每个顶点执行一次Dijkstra算法,时间复杂度就是$( O(\vert V\vert^3) )$有向无环图描述表达式 有向⽆环图:若⼀个有向图中不存在环,则称为有向⽆环图,简称DAG图(Directed Acyclic Graph) 如下图是$((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e)$的二叉树表示和有向无环图表示 有向无环图描述表达式示意图图片 拓扑排序 AOV网(Activity On Vertex Network,顶点表示活动的网络):用有向无环图(DAG)来表示一个工程。顶点表示活动,有向边 $\langle V_i, V_j \rangle$ 表示活动 $V_i$ 必须先于活动 $V_j$ 进行。 拓扑排序:在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序: 每个顶点出现且只出现一次。 若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径。 或定义为:拓扑排序是对有向无环图的顶点的一种排序,它使得若存在一条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。 拓扑排序的算法步骤如下: 从DAG图中选择一个没有前驱的顶点并输出 从图中删除该顶点和所有以它为起点的边 重复上述过程直到当前为空或不存在无前驱的顶点(有环)为止 如下图是一个拓扑排序的例子: 拓扑排序示例图片 如下是基于邻接表的拓扑排序实现: void TopologicalSort(ALGraph G) { InitStack(S); for (int i = 0; i < G.vexnum; i++) { if (G.vexs[i].in == 0) {// 如果顶点的入度为0 Push(S, i); // 将顶点入栈 } } int count = 0; // 计数器,记录已输出的顶点数 while (!StackEmpty(S)) { Pop(S, v); // 栈顶元素出栈 printf("%c ", G.vexs[v].data); // 输出顶点 count++;// 已输出顶点数加1 for(p=G.vexs[v].first;p!=NULL;p=p->next){ //将所有v指向的顶点的入度减1 w = p->adjvex; // 获取邻接点 if(--G.vexs[w].in==0) { // 如果入度减为0 Push(S, w); // 将入度为0的顶点入栈 } } } if(count<G.vexnum) { printf("图中存在环,无法进行拓扑排序。\n"); } else { printf("\n拓扑排序完成。\n"); } } 时间复杂度:$O(|V| + |E|)$(邻接表实现),$O(|V|^2)$(邻接矩阵实现) 排序结果不唯一 工程可以从入度为0的顶点开始(不存在前驱) 对于一般的图来说,其邻接矩阵是三角矩阵,则存在拓扑排序;反之不一定成立。 逆拓扑排序:拓扑排序的逆序称为逆拓扑排序。具体过程就是把出度为0的顶点输出,删除该点和以该点为终点的有向边。关键路径 在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为⽤边表示活动的⽹络,简称AOE⽹ (Activity On Edge NetWork) AOE⽹具有以下两个性质: 只有在某顶点所代表的事件发⽣后,从该顶点出发的各有向边所代表的活动才能开始; 只有在进⼊某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发⽣。另外,有些活动是可以并⾏进⾏的 在AOE⽹中仅有⼀个 ⼊度 为0的顶点,称为开始顶点(源点),它表示整个⼯程的开始。也仅有⼀个出度为0的顶点,称为结束顶点(汇点),它表示整个⼯程的结束。 从源点到汇点的有向路径可能有多条,所有路径中,具有最⼤路径⻓度的路径称为关键路径,⽽把关键路径上的活动称为关键活动,完成整个⼯程的最短时间就是关键路径的⻓度,若关键活动不能按时完成,则整个⼯程的完成时间就会延⻓。 以下是几种参考的量的定义: 事件 $v_k$ 的最早发生时间 $v_e(k)$ 指从开始顶点 $V$ 到事件 $v_k$ 的最长路径长度。计算公式为: $$ v_e(k) = \max \{ v_e(j) + \text{Weight}(v_j, v_k) \} $$其中 $\text{Weight}(v_j, v_k)$ 表示边 $\langle v_j, v_k \rangle$ 的权值。$v_e(k)$ 按从前往后的顺序计算。 事件 $v_k$ 的最迟发生时间 $v_l(k)$ 指在不推迟整个工程完成的前提下,事件 $v_k$ 最迟必须发生的时间。计算公式为: $$ v_l(j) = \min \{ v_l(k) - \text{Weight}(v_j, v_k) \} $$其中 $\text{Weight}(v_j, v_k)$ 表示边 $\langle v_j, v_k \rangle$ 的权值。$v_l(j)$ 按从后往前的顺序计算。 活动 $a_i$ 的最早开始时间 $e(i)$ 即该活动的起点事件的最早发生时间。若边 $\langle v_k, v_j \rangle$ 表示活动 $a_i$,则 $$ e(i) = v_e(k) $$ 活动 $a_i$ 的最迟开始时间 $l(i)$ 即活动终点事件的最迟发生时间减去该活动所需时间。若边 $\langle v_k, v_j \rangle$ 表示活动 $a_i$,则 $$ l(i) = v_l(j) - \text{Weight}(v_k, v_j) $$ 活动 $a_i$ 的时间余量 $d(i)$ 即最迟开始时间与最早开始时间之差: $$ d(i) = l(i) - e(i) $$$d(i)$ 表示在不增加整个工程完成时间的前提下,活动 $a_i$ 可以拖延的最大时间。若 $d(i) = 0$,则该活动为关键活动,必须如期完成。 求关键路径的算法: 求所有$v_e()$ 求所有$v_l()$ 求所有e() 求所有l() 求所有d(),找出关键路径 d(k)=0的活动就是关键活动, 由关键活动可得关键路径 如下图所示是一个求解关键路径的示例: 求解关键路径示例图片 注意以下几点: 关键路径所有活动都是关键活动 关键路径不唯一 加速某一关键活动不一定缩短整个工程的工期.因为AOE网中存在多条关键路径.可能存在称为"桥"的一种特殊关键活动,它位于所有的关键路径上,只有它加速才会缩短整个工期。 番外篇:采用不同存储结构时各种图算法的时间复杂度 存储结构DijkstraFloydPrimKruskalDFSBFS拓扑排序关键路径邻接矩阵$O(n^2)$$O(n^3)$$O(n^2)$-$O(n^2)$$O(n^2)$$O(n^2)$$O(n^2)$邻接表---$O(e\log _2 e)$$O(n+e)$$O(n+e)$$O(n+e)$$O(n+e)$ -
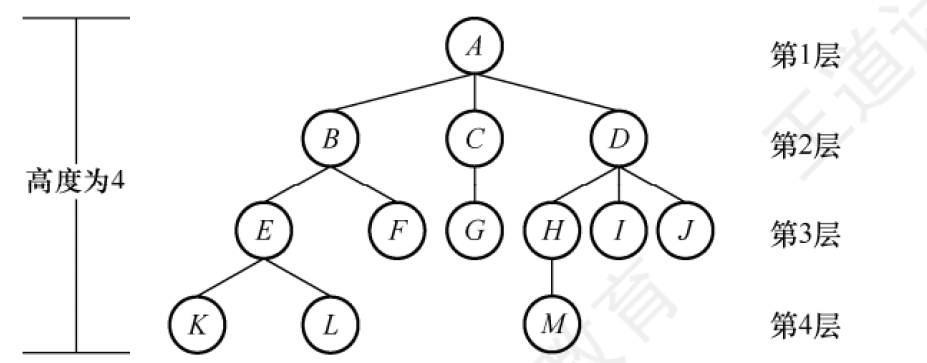
 【计算机考研(408)- 数据结构】树与二叉树 树与二叉树 树的定义及相关概念 树是n(n≥0)个结点的有限集合,n = 0时,称为空树,这是一种特殊情况。在任意一棵非空树中应满足: 1)有且仅有一个特定的称为根的结点。 2)当n > 1时,其余结点可分为m(m > 0)个互不相交的有限集合T1, T2,…, Tm,其中每个集合本身又是一棵树,并且称为根结点的子树。 3)树的根结点没有前驱结点,其余结点有且仅有一个前驱结点。 4)树中所有结点可以有零个或多个后继结点。 树的基本术语 结点之间的关系描述:则有:祖先结点,子孙结点,双亲结点,孩子节点,兄弟结点,堂兄弟结点,以上完全可以按照树的结构和亲戚对应的关系很方便的区分。如图所示: 树的结点之间的关系图片 很明显地可以了解到:B的子孙有EFKL,路径上的ABE都是K的祖先结点,E是K的双亲(父结点),K是E的子孙结点(孩子),K和L具有相同的双亲E,因此K和L是兄弟结点。结点G和EFHIJ互为堂兄弟结点。(排得差不多了,自己领会吧)。 结点、树的属性描述:结点的层次(深度)——从上往下数(从根到该节点的深度,例如B的深度为2),结点的高度——从下往上数,以该结点为根的子树的高度,例如D的高度为3,树的高度(深度)——总共多少层,上图树高度为4,结点的度——有几个孩子(分支),B度为2,D度为3,树的度——各结点的度的最大值。 树中度大于0的结点为分支结点,度为0的结点为叶子结点。在分支结点中,每个结点的分支数就是该结点的度。 有序树——逻辑上看,树中结点的各子树从左至右是有次序的,不能互换。 无序树——逻辑上看,树中结点的各子树从左至右是无次序的,可以互换。 路径——路径是由两个节点之间所经过的结点序列构成的。 路径长度——所经过的边的个数。 森林——森林是m(m≥0)棵互不相交的树的集合。 ^ac8bfc 树的性质 证明我就不写了,留给我自己去推。 树中的结点数等于所有结点的度数加1(加的是根) 度为m的树中第i层至多有$m^{i-1}$个结点 高度为h的m叉树至多有$(m^h-1)/(m-1)$个结点 具有n个结点的m叉树的最小高度为$\lceil log_m(n(m-1)+1)\rceil$ 度为m、具有n个结点的树最大高度为$n-m+1$ 高度为h的m叉树至少有h个结点。高度为h、度为m的树至少有h+m-1个结点。 二叉树的定义及相关概念 二叉树是n(n≥0)个结点的有限集合: 1)或者为空二叉树,即n = 0。 2)或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。 特点:1. 每个结点至多只有两棵子树 2. 左右子树不能颠倒(二叉树是有序树)。 二叉树和度为2的有序树的区别: 度为2的有序树树至少有3个结点,而二叉树可以为空 度为2的有序树的左右次序是相对于另一个孩子结点而言的,若某个结点只有一个孩子结点,则这个孩子结点就无须区分左右次序。而二叉树不一样。 几种特殊的二叉树 满二叉树 满二叉树:高度为h,且含有$2^h-1$个结点。每层都含有最多的结点。除了叶子结点度都为2。 特点: 只有最后一层有叶子结点 不存在度为1的结点 按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1;结点i的父节点为$\lfloor i/2 \rfloor$(如果有的话) 示例图: 满二叉树示例|70%图片 完全二叉树 完全二叉树:当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。 有n个结点。特点如下: 若 $i \leq \lceil n/2 \rceil$,则结点 $i$ 为分支结点,否则为叶子结点。 只有最后两层才会出现叶子结点。 最多只有一个度为 1 的结点(这种情况下该结点一定只有左孩子,没有右孩子)。 按层序编号,若 $i$ 结点为叶子结点或只有左孩子,则编号大于 $i$ 的结点均为叶子结点。 同满二叉树的3.特点。 示例图: 完全二叉树示例|70%图片 完全二叉树可以视作从满二叉树中删去若干最底层、最右边的一些连续叶节点所得到的二叉树。平衡二叉树 平衡二叉树:任意结点的左右子树的深度之差不超过1。详见 二叉排序树 二叉排序树:左子树上所有结点均小于根结点的关键字;右子树所有结点均大于根结点的关键字。左子树和右子树个是一棵二叉排序树。详见 正则二叉树 正则二叉树:树中每个分支都有两个孩子,即树中只有度为0或2的结点。 二叉树的性质 以下推导过程略,自己推。 非空二叉树的叶子结点数等于度为2的结点数加1,即$n_0=n_2+1$ 非空二叉树第i层最多有$2^{i-1}$个结点->m叉树第i层最多有$m^{i-1}$个结点 高度为h的二叉树至多有$2^h-1$个结点(为一棵满二叉树)->高度为h的m叉树至多有$(m^h-1)/(m-1)$个结点 具有n个结点的完全二叉树的高度$\lceil log_2(n+1)\rceil$或$\lfloor log_2n\rfloor+1$ 若完全二叉树有2k个(偶数)个结点,则必有$n_1=1$,$n_0 = k$,$n_2 = k-1$,若完全二叉树有2k-1个(奇数)个结点,则必有$n_1=0$,$n_0=k$,$n_2=k-1$(突破点:完全二叉树最多只会有一个度为1的结点) 二叉树的存储结构 二叉树的顺序存储结构 顺序存储结构:用一组地址连续的存储单元一次自上而下、自左至右存储完全二叉树的结点元素。即完全二叉树编号为i的结点元素存储在某个数组下标为i-1的分量中。该结构对顺序二叉树和完全二叉树比较合适。这种存储结构要从数组下标1开始存储数中的结点。 二叉树的顺序存储中,一定要把二叉树的结点编号与完全二叉树对应起来,所以一定会有大量的空间被浪费掉。 基于以上特点如果用来存储满二叉树和完全二叉树可能使用此方法较为适合。 二叉树的顺序存储结构图片 二叉树的链式存储结构 由于顺序存储的空间利用率较低,所以我们一般都会采用链式存储结构。用链表结点来存储二叉树的每个结点。如图所示一个二叉树链式存储的结点结构。 二叉树链式存储的结点结构图片 二叉树的链式存储结构描述如下: typedef struct BiTNode { ElemType data; // 结点数据 struct BiTNode *lchild, *rchild; // 左右孩子指针 } BiTNode, *BiTree;一颗二叉树及其所对应的二叉链表如图所示,展示了链式存储结构: 一颗二叉树及其所对应的二叉链表图片 当然也很容易知道,含有n个结点的二叉链表中,含有n+1个空链域。这为后面的线索二叉树提供了方便。二叉树的遍历 先序遍历 先序遍历:先访问根结点,然后先序遍历左子树,最后先序遍历右子树。 实现: void PreOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 visit(T); // 访问根结点 PreOrderTraverse(T->lchild); // 先序遍历左子树 PreOrderTraverse(T->rchild); // 先序遍历右子树 }中序遍历 中序遍历:先中序遍历左子树,然后访问根结点,最后中序遍历右子树。 实现: void InOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 InOrderTraverse(T->lchild); // 中序遍历左子树 visit(T); // 访问根结点 InOrderTraverse(T->rchild); // 中序遍历右子树 }后序遍历 后序遍历:先后序遍历左子树,然后后序遍历右子树,最后访问根结点。 实现: void PostOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 PostOrderTraverse(T->lchild); // 后序遍历左子树 PostOrderTraverse(T->rchild); // 后序遍历右子树 visit(T); // 访问根结点 }层次遍历 层次遍历:从根结点开始,按层次顺序访问结点。 实现: void LevelOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 Queue<BiTree> q;//这里需要用到一个辅助队列 q.push(T); while (!q.empty()) { BiTree node = q.front(); q.pop(); visit(node); if (node->lchild != NULL) q.push(node->lchild); if (node->rchild != NULL) q.push(node->rchild); } }这里用到了之前已经学过的[[栈和队列#队列]]的知识,代码里面用到了C++的队列,如果是书上的,那么 push就是 EnQueue,pop就是 DeQueue。 算法效率分析与改造 不管是哪种算法,每个结点都访问一次且仅访问一次,故时间复杂度都是O(n)。 算法改造成为非递归算法时,通常需要借用[[栈和队列#栈]]一个来存储结点。如以下中序遍历改造所示: // 中序遍历非递归算法,需要借用一个栈 void InOrder2(BiTree T){ InitStack(S); BiTree p=T; // p是遍历指针 while(p||!isEmpty(S)){ if(p){ Push(S,p); p=p->lchild; } else{ Pop(S,p); visit(p); p=p->rchild; } } }利用遍历序列构造一个二叉树 给定先序遍历和中序遍历序列,可以唯一确定一棵二叉树。先序遍历的第一个元素是根结点,然后在中序遍历中找到根结点的位置,左边的部分是左子树,右边的部分是右子树。 同理,给定后序遍历和中序遍历序列,也可以唯一确定一棵二叉树。后序遍历的最后一个元素是根结点,然后在中序遍历中找到根结点的位置,左边的部分是左子树,右边的部分是右子树。 那么,给定层序和中序遍历,也可以唯一确定一棵二叉树。层序遍历的第一个元素是根结点,然后在中序遍历中找到根结点位置,左边的部分是左子树,右边的部分是右子树。 那么很显然,先序、后序、层序俩俩组合无法唯一确定一棵二叉树。 注:此节需要练习才能熟练掌握。 线索二叉树 传统的二叉树,每个结点有两个指针,分别指向左孩子和右孩子。不能直接得到结点在遍历过程中的前驱和后继结点。为了解决这个问题,引入了线索二叉树。 在前面的内容中我们知道:在含有n个结点的二叉树中,含有n+1个空链域。线索二叉树就是利用这些空链域来存储结点的前驱和后继信息。 线索二叉树规定:若无左子树,令lchild指向其前驱结点;若无右子树,令rchild指向其后继结点。如图所示为线索二叉树的结点结构 线索二叉树的结点结构图片 其中标志域lflag和rflag用来标识指针域是指向孩子结点还是前驱/后继结点。 $$ \begin{array}{l} \left\{ \begin{aligned} &\text{lflag}=0 \text{ 表示 } lchild \text{ 指向孩子结点} \\ &\text{lflag}=1 \text{ 表示 } lchild \text{ 指向前驱结点} \\ &\text{rflag}=0 \text{ 表示 } rchild \text{ 指向孩子结点} \\ &\text{rflag}=1 \text{ 表示 } rchild \text{ 指向后继结点} \\ \end{aligned} \right. \end{array} $$那么线索二叉树的存储结构描述如下: typedef struct ThreadNode { ElemType data; // 结点数据 struct ThreadNode *lchild, *rchild; // 左右孩子指针 int lflag, rflag; // 标志域 } ThreadNode, *ThreadTree;线索二叉树的构造:遍历一次二叉树,只是在遍历的过程中,检查当前结点的左右指针域是否为空,若为空,将它们改为指向前驱结点或后继结点的线索。代码: // 创建中序线索二叉树 void CreateInThread(ThreadTree T) { ThreadTree pre = NULL; // pre用于记录当前结点的前驱 if (T != NULL) { InThread(T, pre); // 对二叉树进行中序线索化 pre->rchild = NULL; // 最后一个结点的后继线索置空 pre->rtag = 1; // rtag=1表示rchild为线索 } } // 中序遍历递归线索化 void InThread(ThreadTree &p, ThreadTree &pre) { if (p != NULL) { InThread(p->lchild, pre); // 递归线索化左子树 // 若左子树为空,则lchild指向前驱pre,ltag=1 if (p->lchild == NULL) { p->lchild = pre; p->ltag = 1; } // 若前驱结点的右子树为空,则rchild指向当前结点,rtag=1 if (pre != NULL && pre->rchild == NULL) { pre->rchild = p; pre->rtag = 1; } pre = p; // 更新前驱为当前结点 InThread(p->rchild, pre); // 递归线索化右子树 } }先序线索化: void CreatePreThread(ThreadTree T) { ThreadTree pre = NULL; // pre用于记录当前结点的前驱 if (T != NULL) { PreThread(T, pre); // 对二叉树进行先序线索化 if(pre->rchild == NULL) {//这里我有点疑问,可能他和中序线索化一样也不是不行,因为先和中的pre->rchild一定是NULL。 pre->rtag = 1; // rtag=1表示rchild为线索 } } } // 先序遍历递归线索化 void PreThread(ThreadTree p, ThreadTree &pre) { if (p != NULL) { //左子树为空,建立线索 if(p->lchild == NULL){ p->lchild = pre; p->ltag = 1; } if(pre != NULL && pre->rchild == NULL){ pre->rchild = p; pre->rtag = 1; } pre = p; //我们前面介绍过,如果p的左子树为空,则建立p为左孩子,所以判断p的左子树代表的是否为线索 if(p->ltag == 0) { PreThread(p->lchild, pre); // 递归线索化左子树 } PreThread(p->rchild, pre); // 递归线索化右子树 } }后序线索化: void CreatePostThread(ThreadTree T) { ThreadTree pre = NULL; // pre用于记录当前结点的前驱 if (T != NULL) { PostThread(T, pre); // 对二叉树进行后序线索化 if(pre->rchild == NULL) { pre->rtag = 1; // rtag=1表示rchild为 } } } // 后序遍历递归线索化 void PostThread(ThreadTree p, ThreadTree &pre) { if (p != NULL) { PostThread(p->lchild, pre); PostThread(p->rchild, pre); if (p->lchild == NULL) { p->ltag = 1; p->lchild = pre; // 左子树为空,建立线索 } if (pre != NULL && pre->rchild == NULL) { pre->rtag = 1; pre->rchild = p; } pre=p; } }带有头结点的线索二叉树 如图(此为中序): 带有头结点的线索二叉树图片 他的指向关系在图中很明确,这样做的好处就是能够很方便的从前往后或者从后往前对线索二叉树进行一个遍历。 线索二叉树的遍历 线索二叉树的遍历:利用线索二叉树,可以实现二叉树遍历的非递归算法。 以中序遍历找后继为例,代码如下: void Inorder(ThreadNode *T) { for (ThreadNode *p = Firstnode(T); p != NULL; p = Nextnode(p)) visit(p); // 访问结点 } ThreadNode *Firstnode(ThreadNode *p) { while (p->ltag == 0) p = p->lchild; //找到最左下结点 return p; } ThreadNode *Nextnode(ThreadNode *p) { if (p->rtag == 0) return Firstnode(p->rchild); else return p->rchild; // 返回后继结点 }对于中序线索二叉树的遍历,可以使用上述的实现方式,只需变化一些条件,具体可以练习。 对于先序和后序线索二叉树的遍历,类似的实现方式也可以使用。 树和森林 树的存储结构 双亲表示法 采用一组连续空间来存储每个结点,同时每个结点中增设一个伪指针,指示其双亲结点在数组中的位置。可以很快得到每个结点的双亲结点,但求结点的孩子时需要遍历整个结构。 树的双亲表示法图片 存储结构描述: #define MAX_TREE_SIZE 100 // 定义树的最大结点数 typedef struct { ElemType data; // 结点数据 int parent; // 双亲结点的下标 } PTNode; // 双亲结点结构 typedef struct { PTNode nodes[MAX_TREE_SIZE]; // 存储结点的数组 int n; // 结点数 } PTree; // 双亲表示法的树结构双亲表示法表示一个森林:每棵树的根节点双亲指针= -1孩子表示法 将每个结点的孩子结点都用单链表连接起来形成一个线性结构,n个结点就有n个孩子链表。寻找子女操作非常直接,而寻找双亲需要遍历n个结点中孩子链表指针域所指向的n个孩子链表 树的孩子表示法图片 孩子表示法表示一个森林:用孩子表示法存储森林,需要记录多个根的位置孩子兄弟表示法 又称二叉树表示法,即以二叉链表作为树的存储结构。每个结点分为三部分:结点值、指向结点第一个孩子节点的指针,指向结点下一个兄弟结点的指针。优点是可以方便地实现树转换为二叉树的操作,易于查找结点的孩子等。缺点是查找双亲麻烦 孩子兄弟表示法图片 存储结构描述: typedef struct CSNode { ElemType data; // 结点数据 struct CSNode *firstchild; // 指向第一个孩子结点的指针 struct CSNode *nextsibling; // 指向下一个兄弟结点的指针 } CSNode, *CSTree; // 孩子兄弟表示法树、森林转化成二叉树 树转换为二叉树的规则:每个结点左指针指向它的第一个孩子结点,右指针指向它在树中相邻的兄弟节点,“左孩子右兄弟”,由树转换的二叉树没有右子树。 森林转换为二叉树:先将森林中的每棵树转换为二叉树,把第一棵树的根作为转换后二叉树的根,其左子树作为左子树。第二棵树作为转换后的右子树,第三棵树作为转换后右子树的右子树,即向右拼接。 二叉树转换为森林/树的规则:反过来即可。将右子树挨个拆下来。二叉树转换为树或森林是唯一的。 树和森林的遍历 树和森林遍历与二叉树遍历之前的对应关系 树森林二叉树先根遍历先序遍历先序遍历后根遍历后序遍历中序遍历树与二叉树的应用 哈夫曼树和哈夫曼编码 结点的权:有某种现实含义的数值(如:表示结点的重要性等) 结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积 树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL, Weighted Path Length) $$WPL=\sum_{i=1}^{n} w_i \cdot l_i$$ 在含有n个带权叶节点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树(Huffman Tree),也称为最优二叉树。 例题: 具有不同带权长度的二叉树图片 由此算得: $WPL_a=7*2+5*2+2*2+4*2=36$ $WPL_b=7*3+5*3+2*1+4*2=46$ $WPL_c=7*1+5*2+2*3+4*3=35$(哈夫曼树) 构造方式:简单说,从结点中选出两个最小的结点,构成一个新节点,权为两结点之和,重复直到所有结点都处理完毕。 哈夫曼编码就是左0右1,那么a=0 ;b=10;c=110;d=111。 哈夫曼编码的特点是:没有一个编码是另一个编码的前缀,这样可以保证编码的唯一性。 并查集 并查集的概念及其实现 并查集是一种简单的集合表示,它支持以下操作:Initialize(初始化)、Find(查找)、Union(合并)。 并查集的存储结构 通常用树的双亲表示作为并查集的存储结构,每个子集合以一棵树表示。多说无益,直接看示意图: 假设有一个S={0,1,2,3,4,5,6,7,8,9,10},初始化他们都是一个个的几个,每个子集合的数组值为-1。 初始表示: 初始图片 经过系列计算以后,他们合并成为了三个集合:$S_1=\{0,6,7,8\}$、$S_2=\{1,4,9\}$、$S_3=\{2,3,5\}$ 计算1图片 又计算,想把$S_1$和$S_2$合并 计算2图片 结束,很一目了然的并查集 并查集操作的基本实现 #define MAX_SIZE 100 // 并查集的最大大小 int UFSets[MAX_SIZE];// 并查集数组(双亲表示法) //初始化 void InitUFSets() { for (int i = 0; i < MAX_SIZE; i++) UFSets[i] = -1; // 每个元素初始化为-1,表示每个元素都是一个独立的集合 } //Find 找到集合的根元素 int Find(int x) { while (UFSets[x] >= 0) x = UFSets[x]; return x; } //Union 合并两个集合 void Union(int Root1, int Root2) { if (Root1 != Root2) {//要求Root1和Root2是不同的集合 UFSets[Root2] = Root1; // 将Root2的根元素指向Root1,表示合并 } }注意:本代码并没有传递数组参数,因为只是一整个代码,已经放在全局变量中,遇到题目需要自行分析。 复杂度分析:Find操作的时间复杂度为$O(d)$(d为树深度),Union操作的时间复杂度为O(1)。并查集之优化 //改进后的Union void Union(int Root1, int Root2) { if(Root1 != Root2) { //要求Root1和Root2是不同的集合 if (UFSets[Root1] < UFSets[Root2]) { // Root1的集合更大 UFSets[Root1] += UFSets[Root2]; // 更新Root1的大小 UFSets[Root2] = Root1; // 将Root2的根元素指向Root1 } else { UFSets[Root2] += UFSets[Root1]; // 更新Root2的大小 UFSets[Root1] = Root2; // 将Root1的根元素指向Root2 } } } //改进后的Find,目的在于压缩路径,只要是根的元素,就把他挂在根元素上。 int Find(int x) { int root = x; while(UFSets[root] >= 0) { root = UFSets[root]; // 找到根元素 } while(x!=root){ int temp = UFSets[x]; // 临时存储当前元素的父节点 UFSets[x] = root; // 路径压缩,将当前元素直接指向根元素 x = temp; // 移动到下一个元素 } return root; }
【计算机考研(408)- 数据结构】树与二叉树 树与二叉树 树的定义及相关概念 树是n(n≥0)个结点的有限集合,n = 0时,称为空树,这是一种特殊情况。在任意一棵非空树中应满足: 1)有且仅有一个特定的称为根的结点。 2)当n > 1时,其余结点可分为m(m > 0)个互不相交的有限集合T1, T2,…, Tm,其中每个集合本身又是一棵树,并且称为根结点的子树。 3)树的根结点没有前驱结点,其余结点有且仅有一个前驱结点。 4)树中所有结点可以有零个或多个后继结点。 树的基本术语 结点之间的关系描述:则有:祖先结点,子孙结点,双亲结点,孩子节点,兄弟结点,堂兄弟结点,以上完全可以按照树的结构和亲戚对应的关系很方便的区分。如图所示: 树的结点之间的关系图片 很明显地可以了解到:B的子孙有EFKL,路径上的ABE都是K的祖先结点,E是K的双亲(父结点),K是E的子孙结点(孩子),K和L具有相同的双亲E,因此K和L是兄弟结点。结点G和EFHIJ互为堂兄弟结点。(排得差不多了,自己领会吧)。 结点、树的属性描述:结点的层次(深度)——从上往下数(从根到该节点的深度,例如B的深度为2),结点的高度——从下往上数,以该结点为根的子树的高度,例如D的高度为3,树的高度(深度)——总共多少层,上图树高度为4,结点的度——有几个孩子(分支),B度为2,D度为3,树的度——各结点的度的最大值。 树中度大于0的结点为分支结点,度为0的结点为叶子结点。在分支结点中,每个结点的分支数就是该结点的度。 有序树——逻辑上看,树中结点的各子树从左至右是有次序的,不能互换。 无序树——逻辑上看,树中结点的各子树从左至右是无次序的,可以互换。 路径——路径是由两个节点之间所经过的结点序列构成的。 路径长度——所经过的边的个数。 森林——森林是m(m≥0)棵互不相交的树的集合。 ^ac8bfc 树的性质 证明我就不写了,留给我自己去推。 树中的结点数等于所有结点的度数加1(加的是根) 度为m的树中第i层至多有$m^{i-1}$个结点 高度为h的m叉树至多有$(m^h-1)/(m-1)$个结点 具有n个结点的m叉树的最小高度为$\lceil log_m(n(m-1)+1)\rceil$ 度为m、具有n个结点的树最大高度为$n-m+1$ 高度为h的m叉树至少有h个结点。高度为h、度为m的树至少有h+m-1个结点。 二叉树的定义及相关概念 二叉树是n(n≥0)个结点的有限集合: 1)或者为空二叉树,即n = 0。 2)或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。 特点:1. 每个结点至多只有两棵子树 2. 左右子树不能颠倒(二叉树是有序树)。 二叉树和度为2的有序树的区别: 度为2的有序树树至少有3个结点,而二叉树可以为空 度为2的有序树的左右次序是相对于另一个孩子结点而言的,若某个结点只有一个孩子结点,则这个孩子结点就无须区分左右次序。而二叉树不一样。 几种特殊的二叉树 满二叉树 满二叉树:高度为h,且含有$2^h-1$个结点。每层都含有最多的结点。除了叶子结点度都为2。 特点: 只有最后一层有叶子结点 不存在度为1的结点 按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1;结点i的父节点为$\lfloor i/2 \rfloor$(如果有的话) 示例图: 满二叉树示例|70%图片 完全二叉树 完全二叉树:当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。 有n个结点。特点如下: 若 $i \leq \lceil n/2 \rceil$,则结点 $i$ 为分支结点,否则为叶子结点。 只有最后两层才会出现叶子结点。 最多只有一个度为 1 的结点(这种情况下该结点一定只有左孩子,没有右孩子)。 按层序编号,若 $i$ 结点为叶子结点或只有左孩子,则编号大于 $i$ 的结点均为叶子结点。 同满二叉树的3.特点。 示例图: 完全二叉树示例|70%图片 完全二叉树可以视作从满二叉树中删去若干最底层、最右边的一些连续叶节点所得到的二叉树。平衡二叉树 平衡二叉树:任意结点的左右子树的深度之差不超过1。详见 二叉排序树 二叉排序树:左子树上所有结点均小于根结点的关键字;右子树所有结点均大于根结点的关键字。左子树和右子树个是一棵二叉排序树。详见 正则二叉树 正则二叉树:树中每个分支都有两个孩子,即树中只有度为0或2的结点。 二叉树的性质 以下推导过程略,自己推。 非空二叉树的叶子结点数等于度为2的结点数加1,即$n_0=n_2+1$ 非空二叉树第i层最多有$2^{i-1}$个结点->m叉树第i层最多有$m^{i-1}$个结点 高度为h的二叉树至多有$2^h-1$个结点(为一棵满二叉树)->高度为h的m叉树至多有$(m^h-1)/(m-1)$个结点 具有n个结点的完全二叉树的高度$\lceil log_2(n+1)\rceil$或$\lfloor log_2n\rfloor+1$ 若完全二叉树有2k个(偶数)个结点,则必有$n_1=1$,$n_0 = k$,$n_2 = k-1$,若完全二叉树有2k-1个(奇数)个结点,则必有$n_1=0$,$n_0=k$,$n_2=k-1$(突破点:完全二叉树最多只会有一个度为1的结点) 二叉树的存储结构 二叉树的顺序存储结构 顺序存储结构:用一组地址连续的存储单元一次自上而下、自左至右存储完全二叉树的结点元素。即完全二叉树编号为i的结点元素存储在某个数组下标为i-1的分量中。该结构对顺序二叉树和完全二叉树比较合适。这种存储结构要从数组下标1开始存储数中的结点。 二叉树的顺序存储中,一定要把二叉树的结点编号与完全二叉树对应起来,所以一定会有大量的空间被浪费掉。 基于以上特点如果用来存储满二叉树和完全二叉树可能使用此方法较为适合。 二叉树的顺序存储结构图片 二叉树的链式存储结构 由于顺序存储的空间利用率较低,所以我们一般都会采用链式存储结构。用链表结点来存储二叉树的每个结点。如图所示一个二叉树链式存储的结点结构。 二叉树链式存储的结点结构图片 二叉树的链式存储结构描述如下: typedef struct BiTNode { ElemType data; // 结点数据 struct BiTNode *lchild, *rchild; // 左右孩子指针 } BiTNode, *BiTree;一颗二叉树及其所对应的二叉链表如图所示,展示了链式存储结构: 一颗二叉树及其所对应的二叉链表图片 当然也很容易知道,含有n个结点的二叉链表中,含有n+1个空链域。这为后面的线索二叉树提供了方便。二叉树的遍历 先序遍历 先序遍历:先访问根结点,然后先序遍历左子树,最后先序遍历右子树。 实现: void PreOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 visit(T); // 访问根结点 PreOrderTraverse(T->lchild); // 先序遍历左子树 PreOrderTraverse(T->rchild); // 先序遍历右子树 }中序遍历 中序遍历:先中序遍历左子树,然后访问根结点,最后中序遍历右子树。 实现: void InOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 InOrderTraverse(T->lchild); // 中序遍历左子树 visit(T); // 访问根结点 InOrderTraverse(T->rchild); // 中序遍历右子树 }后序遍历 后序遍历:先后序遍历左子树,然后后序遍历右子树,最后访问根结点。 实现: void PostOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 PostOrderTraverse(T->lchild); // 后序遍历左子树 PostOrderTraverse(T->rchild); // 后序遍历右子树 visit(T); // 访问根结点 }层次遍历 层次遍历:从根结点开始,按层次顺序访问结点。 实现: void LevelOrderTraverse(BiTree T) { if (T == NULL) return; // 递归终止条件 Queue<BiTree> q;//这里需要用到一个辅助队列 q.push(T); while (!q.empty()) { BiTree node = q.front(); q.pop(); visit(node); if (node->lchild != NULL) q.push(node->lchild); if (node->rchild != NULL) q.push(node->rchild); } }这里用到了之前已经学过的[[栈和队列#队列]]的知识,代码里面用到了C++的队列,如果是书上的,那么 push就是 EnQueue,pop就是 DeQueue。 算法效率分析与改造 不管是哪种算法,每个结点都访问一次且仅访问一次,故时间复杂度都是O(n)。 算法改造成为非递归算法时,通常需要借用[[栈和队列#栈]]一个来存储结点。如以下中序遍历改造所示: // 中序遍历非递归算法,需要借用一个栈 void InOrder2(BiTree T){ InitStack(S); BiTree p=T; // p是遍历指针 while(p||!isEmpty(S)){ if(p){ Push(S,p); p=p->lchild; } else{ Pop(S,p); visit(p); p=p->rchild; } } }利用遍历序列构造一个二叉树 给定先序遍历和中序遍历序列,可以唯一确定一棵二叉树。先序遍历的第一个元素是根结点,然后在中序遍历中找到根结点的位置,左边的部分是左子树,右边的部分是右子树。 同理,给定后序遍历和中序遍历序列,也可以唯一确定一棵二叉树。后序遍历的最后一个元素是根结点,然后在中序遍历中找到根结点的位置,左边的部分是左子树,右边的部分是右子树。 那么,给定层序和中序遍历,也可以唯一确定一棵二叉树。层序遍历的第一个元素是根结点,然后在中序遍历中找到根结点位置,左边的部分是左子树,右边的部分是右子树。 那么很显然,先序、后序、层序俩俩组合无法唯一确定一棵二叉树。 注:此节需要练习才能熟练掌握。 线索二叉树 传统的二叉树,每个结点有两个指针,分别指向左孩子和右孩子。不能直接得到结点在遍历过程中的前驱和后继结点。为了解决这个问题,引入了线索二叉树。 在前面的内容中我们知道:在含有n个结点的二叉树中,含有n+1个空链域。线索二叉树就是利用这些空链域来存储结点的前驱和后继信息。 线索二叉树规定:若无左子树,令lchild指向其前驱结点;若无右子树,令rchild指向其后继结点。如图所示为线索二叉树的结点结构 线索二叉树的结点结构图片 其中标志域lflag和rflag用来标识指针域是指向孩子结点还是前驱/后继结点。 $$ \begin{array}{l} \left\{ \begin{aligned} &\text{lflag}=0 \text{ 表示 } lchild \text{ 指向孩子结点} \\ &\text{lflag}=1 \text{ 表示 } lchild \text{ 指向前驱结点} \\ &\text{rflag}=0 \text{ 表示 } rchild \text{ 指向孩子结点} \\ &\text{rflag}=1 \text{ 表示 } rchild \text{ 指向后继结点} \\ \end{aligned} \right. \end{array} $$那么线索二叉树的存储结构描述如下: typedef struct ThreadNode { ElemType data; // 结点数据 struct ThreadNode *lchild, *rchild; // 左右孩子指针 int lflag, rflag; // 标志域 } ThreadNode, *ThreadTree;线索二叉树的构造:遍历一次二叉树,只是在遍历的过程中,检查当前结点的左右指针域是否为空,若为空,将它们改为指向前驱结点或后继结点的线索。代码: // 创建中序线索二叉树 void CreateInThread(ThreadTree T) { ThreadTree pre = NULL; // pre用于记录当前结点的前驱 if (T != NULL) { InThread(T, pre); // 对二叉树进行中序线索化 pre->rchild = NULL; // 最后一个结点的后继线索置空 pre->rtag = 1; // rtag=1表示rchild为线索 } } // 中序遍历递归线索化 void InThread(ThreadTree &p, ThreadTree &pre) { if (p != NULL) { InThread(p->lchild, pre); // 递归线索化左子树 // 若左子树为空,则lchild指向前驱pre,ltag=1 if (p->lchild == NULL) { p->lchild = pre; p->ltag = 1; } // 若前驱结点的右子树为空,则rchild指向当前结点,rtag=1 if (pre != NULL && pre->rchild == NULL) { pre->rchild = p; pre->rtag = 1; } pre = p; // 更新前驱为当前结点 InThread(p->rchild, pre); // 递归线索化右子树 } }先序线索化: void CreatePreThread(ThreadTree T) { ThreadTree pre = NULL; // pre用于记录当前结点的前驱 if (T != NULL) { PreThread(T, pre); // 对二叉树进行先序线索化 if(pre->rchild == NULL) {//这里我有点疑问,可能他和中序线索化一样也不是不行,因为先和中的pre->rchild一定是NULL。 pre->rtag = 1; // rtag=1表示rchild为线索 } } } // 先序遍历递归线索化 void PreThread(ThreadTree p, ThreadTree &pre) { if (p != NULL) { //左子树为空,建立线索 if(p->lchild == NULL){ p->lchild = pre; p->ltag = 1; } if(pre != NULL && pre->rchild == NULL){ pre->rchild = p; pre->rtag = 1; } pre = p; //我们前面介绍过,如果p的左子树为空,则建立p为左孩子,所以判断p的左子树代表的是否为线索 if(p->ltag == 0) { PreThread(p->lchild, pre); // 递归线索化左子树 } PreThread(p->rchild, pre); // 递归线索化右子树 } }后序线索化: void CreatePostThread(ThreadTree T) { ThreadTree pre = NULL; // pre用于记录当前结点的前驱 if (T != NULL) { PostThread(T, pre); // 对二叉树进行后序线索化 if(pre->rchild == NULL) { pre->rtag = 1; // rtag=1表示rchild为 } } } // 后序遍历递归线索化 void PostThread(ThreadTree p, ThreadTree &pre) { if (p != NULL) { PostThread(p->lchild, pre); PostThread(p->rchild, pre); if (p->lchild == NULL) { p->ltag = 1; p->lchild = pre; // 左子树为空,建立线索 } if (pre != NULL && pre->rchild == NULL) { pre->rtag = 1; pre->rchild = p; } pre=p; } }带有头结点的线索二叉树 如图(此为中序): 带有头结点的线索二叉树图片 他的指向关系在图中很明确,这样做的好处就是能够很方便的从前往后或者从后往前对线索二叉树进行一个遍历。 线索二叉树的遍历 线索二叉树的遍历:利用线索二叉树,可以实现二叉树遍历的非递归算法。 以中序遍历找后继为例,代码如下: void Inorder(ThreadNode *T) { for (ThreadNode *p = Firstnode(T); p != NULL; p = Nextnode(p)) visit(p); // 访问结点 } ThreadNode *Firstnode(ThreadNode *p) { while (p->ltag == 0) p = p->lchild; //找到最左下结点 return p; } ThreadNode *Nextnode(ThreadNode *p) { if (p->rtag == 0) return Firstnode(p->rchild); else return p->rchild; // 返回后继结点 }对于中序线索二叉树的遍历,可以使用上述的实现方式,只需变化一些条件,具体可以练习。 对于先序和后序线索二叉树的遍历,类似的实现方式也可以使用。 树和森林 树的存储结构 双亲表示法 采用一组连续空间来存储每个结点,同时每个结点中增设一个伪指针,指示其双亲结点在数组中的位置。可以很快得到每个结点的双亲结点,但求结点的孩子时需要遍历整个结构。 树的双亲表示法图片 存储结构描述: #define MAX_TREE_SIZE 100 // 定义树的最大结点数 typedef struct { ElemType data; // 结点数据 int parent; // 双亲结点的下标 } PTNode; // 双亲结点结构 typedef struct { PTNode nodes[MAX_TREE_SIZE]; // 存储结点的数组 int n; // 结点数 } PTree; // 双亲表示法的树结构双亲表示法表示一个森林:每棵树的根节点双亲指针= -1孩子表示法 将每个结点的孩子结点都用单链表连接起来形成一个线性结构,n个结点就有n个孩子链表。寻找子女操作非常直接,而寻找双亲需要遍历n个结点中孩子链表指针域所指向的n个孩子链表 树的孩子表示法图片 孩子表示法表示一个森林:用孩子表示法存储森林,需要记录多个根的位置孩子兄弟表示法 又称二叉树表示法,即以二叉链表作为树的存储结构。每个结点分为三部分:结点值、指向结点第一个孩子节点的指针,指向结点下一个兄弟结点的指针。优点是可以方便地实现树转换为二叉树的操作,易于查找结点的孩子等。缺点是查找双亲麻烦 孩子兄弟表示法图片 存储结构描述: typedef struct CSNode { ElemType data; // 结点数据 struct CSNode *firstchild; // 指向第一个孩子结点的指针 struct CSNode *nextsibling; // 指向下一个兄弟结点的指针 } CSNode, *CSTree; // 孩子兄弟表示法树、森林转化成二叉树 树转换为二叉树的规则:每个结点左指针指向它的第一个孩子结点,右指针指向它在树中相邻的兄弟节点,“左孩子右兄弟”,由树转换的二叉树没有右子树。 森林转换为二叉树:先将森林中的每棵树转换为二叉树,把第一棵树的根作为转换后二叉树的根,其左子树作为左子树。第二棵树作为转换后的右子树,第三棵树作为转换后右子树的右子树,即向右拼接。 二叉树转换为森林/树的规则:反过来即可。将右子树挨个拆下来。二叉树转换为树或森林是唯一的。 树和森林的遍历 树和森林遍历与二叉树遍历之前的对应关系 树森林二叉树先根遍历先序遍历先序遍历后根遍历后序遍历中序遍历树与二叉树的应用 哈夫曼树和哈夫曼编码 结点的权:有某种现实含义的数值(如:表示结点的重要性等) 结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积 树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL, Weighted Path Length) $$WPL=\sum_{i=1}^{n} w_i \cdot l_i$$ 在含有n个带权叶节点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树(Huffman Tree),也称为最优二叉树。 例题: 具有不同带权长度的二叉树图片 由此算得: $WPL_a=7*2+5*2+2*2+4*2=36$ $WPL_b=7*3+5*3+2*1+4*2=46$ $WPL_c=7*1+5*2+2*3+4*3=35$(哈夫曼树) 构造方式:简单说,从结点中选出两个最小的结点,构成一个新节点,权为两结点之和,重复直到所有结点都处理完毕。 哈夫曼编码就是左0右1,那么a=0 ;b=10;c=110;d=111。 哈夫曼编码的特点是:没有一个编码是另一个编码的前缀,这样可以保证编码的唯一性。 并查集 并查集的概念及其实现 并查集是一种简单的集合表示,它支持以下操作:Initialize(初始化)、Find(查找)、Union(合并)。 并查集的存储结构 通常用树的双亲表示作为并查集的存储结构,每个子集合以一棵树表示。多说无益,直接看示意图: 假设有一个S={0,1,2,3,4,5,6,7,8,9,10},初始化他们都是一个个的几个,每个子集合的数组值为-1。 初始表示: 初始图片 经过系列计算以后,他们合并成为了三个集合:$S_1=\{0,6,7,8\}$、$S_2=\{1,4,9\}$、$S_3=\{2,3,5\}$ 计算1图片 又计算,想把$S_1$和$S_2$合并 计算2图片 结束,很一目了然的并查集 并查集操作的基本实现 #define MAX_SIZE 100 // 并查集的最大大小 int UFSets[MAX_SIZE];// 并查集数组(双亲表示法) //初始化 void InitUFSets() { for (int i = 0; i < MAX_SIZE; i++) UFSets[i] = -1; // 每个元素初始化为-1,表示每个元素都是一个独立的集合 } //Find 找到集合的根元素 int Find(int x) { while (UFSets[x] >= 0) x = UFSets[x]; return x; } //Union 合并两个集合 void Union(int Root1, int Root2) { if (Root1 != Root2) {//要求Root1和Root2是不同的集合 UFSets[Root2] = Root1; // 将Root2的根元素指向Root1,表示合并 } }注意:本代码并没有传递数组参数,因为只是一整个代码,已经放在全局变量中,遇到题目需要自行分析。 复杂度分析:Find操作的时间复杂度为$O(d)$(d为树深度),Union操作的时间复杂度为O(1)。并查集之优化 //改进后的Union void Union(int Root1, int Root2) { if(Root1 != Root2) { //要求Root1和Root2是不同的集合 if (UFSets[Root1] < UFSets[Root2]) { // Root1的集合更大 UFSets[Root1] += UFSets[Root2]; // 更新Root1的大小 UFSets[Root2] = Root1; // 将Root2的根元素指向Root1 } else { UFSets[Root2] += UFSets[Root1]; // 更新Root2的大小 UFSets[Root1] = Root2; // 将Root1的根元素指向Root2 } } } //改进后的Find,目的在于压缩路径,只要是根的元素,就把他挂在根元素上。 int Find(int x) { int root = x; while(UFSets[root] >= 0) { root = UFSets[root]; // 找到根元素 } while(x!=root){ int temp = UFSets[x]; // 临时存储当前元素的父节点 UFSets[x] = root; // 路径压缩,将当前元素直接指向根元素 x = temp; // 移动到下一个元素 } return root; } -
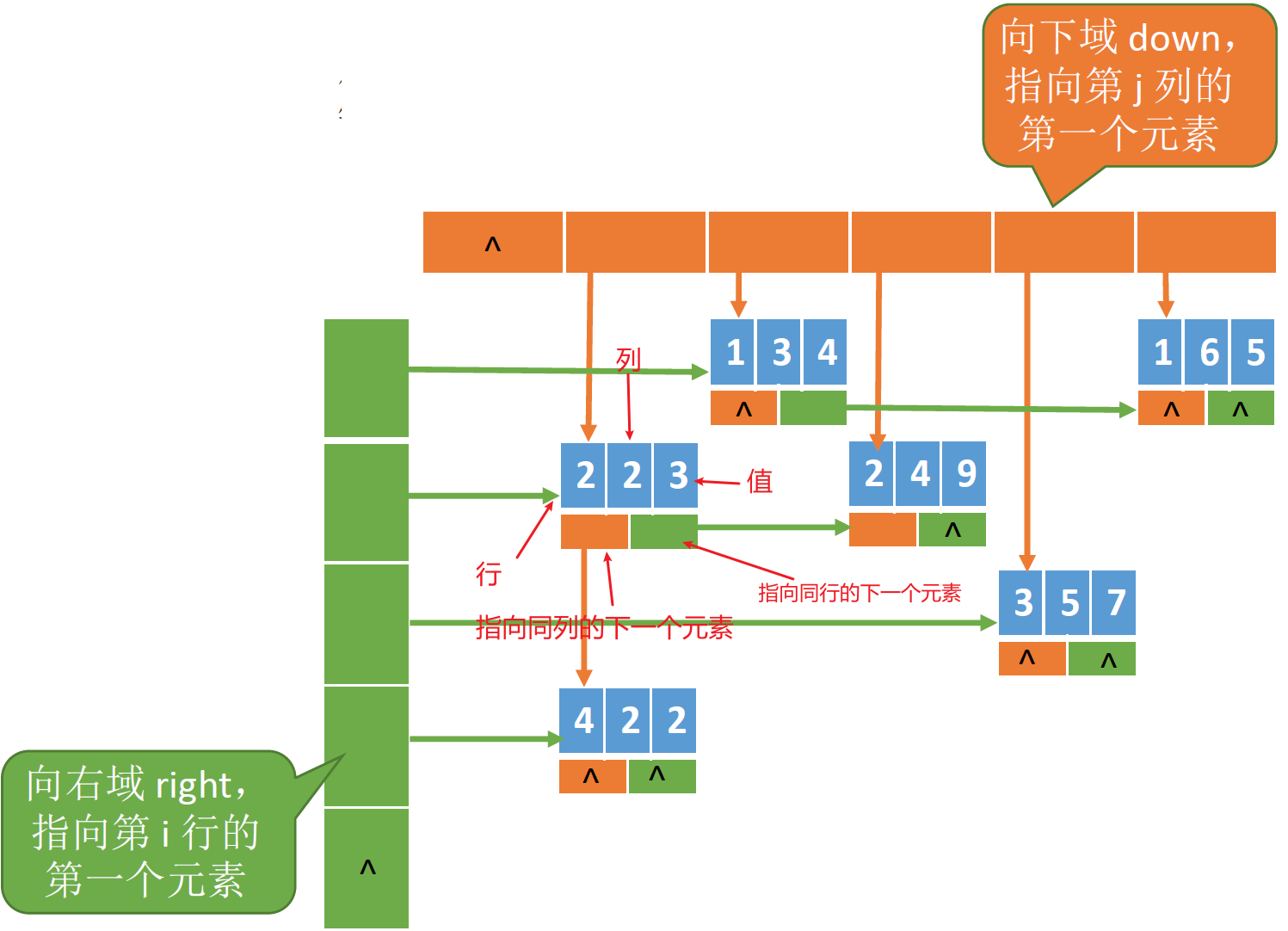
 【计算机考研(408)- 数据结构】数组和特殊矩阵 数组和特殊矩阵 数组 数组的定义 数组是由n(n>=1)个相同类型的数据元素构成的有限序列。每个数据元素称为一个数组元素,每个元素在n个线性关系中的序号称之为该元素的下标,下标的取值范围称为数组的维界。 数组是[[线性表]]的推广,一维数组可视为一个线性表,二维数组可视为其元素是定长数组的线性表。 数组的存储结构 各数组元素大小相同,且物理上连续存放。 我们用一个 Markdown 表格模拟数组的地址存储结构(ElemType a[7]): 其他a[0]a[1]a[2]a[3]a[4]a[5]a[6]其他 LOCLOC+1………………$$ 数组元素a[i]的存放地址= LOC + i * sizeof(ElemType) $$每个单元格表示数组元素在内存中的连续存储位置,数组元素之间没有间隔,便于通过下标快速访问。 接下来假设有一个二维数组() ElemType b[2][4],我们可以用一个 Markdown 表格模拟其地址存储结构和逻辑结构: 逻辑结构: b[0][0]b[0][1]b[0][2]b[0][3]b[1][0]b[1][1]b[1][2]b[1][3]但是在内存中,数组是连续的,那么也就有了行优先和列优先的存储方式。 列优先存储结构: 其他b[0][0]b[1][0]b[0][1]b[1][1]b[0][2]b[1][2]b[0][3]b[1][3]其他…LOC+0LOC+1LOC+2LOC+3LOC+4LOC+5LOC+6LOC+7…M行N列的二维数组b[M][N]中,若按列优先存储,则: $$ b[i][j]的存放地址= LOC + (j * M + i) * sizeof(ElemType) $$行优先存储结构: 其他b[0][0]b[0][1]b[0][2]b[0][3]b[1][0]b[1][1]b[1][2]b[1][3]其他…LOC+0LOC+1LOC+2LOC+3LOC+4LOC+5LOC+6LOC+7…M行N列的二维数组b[M][N]中,若按行优先存储,则: $$ b[i][j]的存放地址= LOC + (i * N + j) * sizeof(ElemType) $$矩阵的存储和特殊矩阵的压缩存储 压缩存储是指为多个值相同的元素只分配一个存储空间,对零元素不分配空间。 特殊矩阵就是指分布有一定规律的矩阵。 压缩存储方法:找出分布规律,把那些呈现规律性分布的、值相同的元素放在同一个存储空间中。 对称矩阵 $a_{1,1}$$a_{1,2}$$\cdots$$a_{1,n}$$a_{2,1}$$a_{2,2}$$\cdots$$a_{2,n}$$\vdots$$\vdots$$\ddots$$\vdots$$a_{n,1}$$a_{n,2}$$\cdots$$a_{n,n}$如上所示的矩阵是一个n阶矩阵,若对于任意的$i,j$,都有$a_{i,j}=a_{j,i}$,则称之为对称矩阵。其中的元素也可以根据i,j的大小分为三个部门:$i=j$主对角线,$i>j$ 下三角区,$i<j$ 上三角区。 普通存储:n*n二维数组,因为上下两个三角区数值相同,所以可以压缩存储。 压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区) 同时我们需要按照行/列优先的原则存入到一个一维数组中,并建立i,j(矩阵下标)与数组下标的映射关系。 以下以行优先为例: 对于i>=j的下标来说,第一个存储的是 i=1,j=1,第二个存储的是 i=2,j=1,接着 2,2、3,1、3,2、3,3。分别映射到了0,1,2,3上面。 根据不难看出,对于i是累加的,比如第一行起始是0,第二行起始是1,到了第三行起始就变为了3。那么其实他就是一个等差数列。 根据等差数列求和公式:$\frac{n(a_1 + a_n)}{2}$,其中$a_1 = 0$,$a_n = i - 1$,$n = i$。因此,第$i$行的起始下标为$\frac{i(i-1)}{2}$。接着我们加上j的偏移量,得到下标为$\frac{i(i-1)}{2} + j - 1$。(j-1的原因是因为数组下标从0开始) 至此我们把矩阵中下三角的元素都存储了,正因为$a_{i,j} = a_{j,i}$,对于上三角的元素,我们直接替换下标即可。 得到最终的下标转换公式如下: $$ k = \begin{cases} \frac{(i-1)i}{2} + j-1, & \text{当 } i \geq j \text{(下三角区和主对角线元素)} \\ \frac{(j-1)j}{2} + i-1, & \text{当 } i < j \text{(上三角区元素)} \end{cases} $$按照上面的方法,分析列优先: 对于i>=j的下标来说,第一个存储的是 i=1,j=1,第二个存储的是 i=1,j=2,接着 2,2、1,3、2,3、3,3。分别映射到了0,1,2,3上面。 根据等差数列求和公式:$\frac{n(a_1 + a_n)}{2}$,其中$a_1 = 0$,$a_n = j - 1$,$n = j$。因此,第$j$列的起始下标为$\frac{j(j-1)}{2}$。接着我们加上i的偏移量,得到下标为$\frac{j(j-1)}{2} + i - 1$。(i-1的原因是因为数组下标从0开始) 至此,我们得到列优先的公式为: $$ k = \begin{cases} \frac{j(j-1)}{2} + i - 1, & \text{if } i \geq j \\ \frac{i(i-1)}{2} + j - 1, & \text{if } i < j \end{cases} $$对于存储上三角的方法,我不想写了,留给我自己思考去吧三角矩阵 $a_{1,1}$$C$$C$$C$$a_{2,1}$$a_{2,2}$$C$$C$$a_{3,1}$$a_{3,2}$$a_{3,3}$$C$$a_{4,1}$$a_{4,2}$$a_{4,3}$$a_{4,4}$下三角矩阵:除了主对角线和下三角区,其余的元素都相同(如表格所示) 上三角矩阵:除了主对角线和上三角区,其余的元素都相同(如表格所示) 压缩存储策略(下三角矩阵为例):按行优先原则将下三角区存入一维数组中。并在最后一个位置存储常量C,上面分析的下三角区存储公式可以直接使用。而常数C的存储位置为$n(n+1)/2$ 存储下三角矩阵的下标转换公式: $$ k = \begin{cases} \frac{(i-1)i}{2} + j - 1, & \ \text{if } i \geq j (下三角区和主对角线元素) \\ \frac{n(n+1)}{2}, & \text{if } i < j (上三角区元素) \end{cases} $$下面开始分析上三角矩阵的存储,还是上面的策略,常数C的存储位置为$n(n+1)/2$。 那么对于第i行应当开始存储的位置应该为上i-1行的元素个数,应当为$n(i-1)-\frac{(i-1)(i-2)}{2}=\frac{(i-1)(2n-i+2)}{2}$,其中,$n(i-1)$代表该矩阵第i行之前一共的元素数目,之后的式子代表下三角区的累计数目,对于第j列,应为相对于对角线的偏移量即为(j-i)。 因此我们可以得到存储上三角矩阵的下标转换公式: $$ k = \begin{cases} \frac{(i-1)(2n-i+2)}{2} + (j-i) & i \leq j (上三角区和主对角线元素) \\ \frac{n(n+1)}{2} & i > j (下三角区元素) \end{cases} $$三对角矩阵 三对角矩阵,又称带状矩阵:当$|i-j|>1$时,元素值为0。$(1\leq i,j\leq n)$ $a_{1,1}$$a_{1,2}$0000$a_{2,1}$$a_{2,2}$$a_{2,3}$0000$a_{3,2}$$a_{3,3}$$a_{3,4}$0000$a_{4,3}$$a_{4,4}$$a_{4,5}$0000$a_{5,4}$$a_{5,5}$$a_{5,6}$0000$a_{6,5}$$a_{6,6}$压缩存储策略:按行优先(或列优先)原则,只存储带状部分 那么按行优先规则,前i-1行的元素个数为$3(i-1)-1$,第i行的元素个数为3,最后一行的元素个数为2。那么$a_{i,j}$是第i行的第j-i+2(如果下标从1开始,从零开始还要减1)个元素。所以我们得到如下的公式: $$ k=3(i-1)-1+j-i+2-1=2i+j-3 $$接下来我们需要讨论一下逆向,即通过k求i和j: 由一维数组下标 $k$ 求矩阵下标 $i, j$ 的方法如下:首先确定行号 $i$,由于前 $i-1$ 行共 $3(i-1)-1$ 个元素,前 $i$ 行共 $3i-1$ 个元素,因此有 $3(i-1)-1 < k+1 \leq 3i-1$,即 $i \geq \frac{k+2}{3}$,向上取整得 $i = \lceil \frac{k+2}{3} \rceil$。 也可以按照王道书的逻辑,$3(i-1)-1 \leq k < 3i-1$,即 $i \leq \frac{k+1}{3} + 1$,向下取整得 $i = \lfloor \frac{k+1}{3} \rfloor + 1$。确定 $i$ 后,前 $i-1$ 行共 $3(i-1)-1$ 个元素,第 $i$ 行的第一个元素下标为 $k_0 = 3(i-1)-1$,所以列号 $j = k - k_0 - 2 + i$。公式总结如下: $$ \begin{aligned} &i = \lceil \frac{k+2}{3} \rceil \\ &j = k - [3(i-1)-1] - 2 + i \end{aligned} $$或者 $$ \begin{aligned} &i = \lfloor \frac{k+1}{3} \rfloor + 1 \\ &j = k - [3(i-1)-1] - 2 + i \end{aligned} $$先根据 $k$ 计算 $i$,再用 $i$ 计算 $j$,两种取整方式结果一致。 稀疏矩阵 稀疏矩阵:非零元素远远少于矩阵元素的个数 压缩存储策略:顺序存储——三元组<行,列,值> 例如,下面的稀疏矩阵: 004005030900000070020000000000其三元组顺序存储形式为:(行、列标从0开始) i行j列v值024055113139247312行、列标从1开始 行列值134165223249357422既然有顺序存储,那么会有链式存储的方式。压缩存储策略二:链式存储——十字链表法 一个结点包含五部分内容:行、列、值、指向下一个同列元素的指针、指向下一个同行元素的指针。 还是上面的矩阵,如果给他创建一个十字链表,那么就会得到如下结果(图源王道课PPT): md1ebaq6.png图片
【计算机考研(408)- 数据结构】数组和特殊矩阵 数组和特殊矩阵 数组 数组的定义 数组是由n(n>=1)个相同类型的数据元素构成的有限序列。每个数据元素称为一个数组元素,每个元素在n个线性关系中的序号称之为该元素的下标,下标的取值范围称为数组的维界。 数组是[[线性表]]的推广,一维数组可视为一个线性表,二维数组可视为其元素是定长数组的线性表。 数组的存储结构 各数组元素大小相同,且物理上连续存放。 我们用一个 Markdown 表格模拟数组的地址存储结构(ElemType a[7]): 其他a[0]a[1]a[2]a[3]a[4]a[5]a[6]其他 LOCLOC+1………………$$ 数组元素a[i]的存放地址= LOC + i * sizeof(ElemType) $$每个单元格表示数组元素在内存中的连续存储位置,数组元素之间没有间隔,便于通过下标快速访问。 接下来假设有一个二维数组() ElemType b[2][4],我们可以用一个 Markdown 表格模拟其地址存储结构和逻辑结构: 逻辑结构: b[0][0]b[0][1]b[0][2]b[0][3]b[1][0]b[1][1]b[1][2]b[1][3]但是在内存中,数组是连续的,那么也就有了行优先和列优先的存储方式。 列优先存储结构: 其他b[0][0]b[1][0]b[0][1]b[1][1]b[0][2]b[1][2]b[0][3]b[1][3]其他…LOC+0LOC+1LOC+2LOC+3LOC+4LOC+5LOC+6LOC+7…M行N列的二维数组b[M][N]中,若按列优先存储,则: $$ b[i][j]的存放地址= LOC + (j * M + i) * sizeof(ElemType) $$行优先存储结构: 其他b[0][0]b[0][1]b[0][2]b[0][3]b[1][0]b[1][1]b[1][2]b[1][3]其他…LOC+0LOC+1LOC+2LOC+3LOC+4LOC+5LOC+6LOC+7…M行N列的二维数组b[M][N]中,若按行优先存储,则: $$ b[i][j]的存放地址= LOC + (i * N + j) * sizeof(ElemType) $$矩阵的存储和特殊矩阵的压缩存储 压缩存储是指为多个值相同的元素只分配一个存储空间,对零元素不分配空间。 特殊矩阵就是指分布有一定规律的矩阵。 压缩存储方法:找出分布规律,把那些呈现规律性分布的、值相同的元素放在同一个存储空间中。 对称矩阵 $a_{1,1}$$a_{1,2}$$\cdots$$a_{1,n}$$a_{2,1}$$a_{2,2}$$\cdots$$a_{2,n}$$\vdots$$\vdots$$\ddots$$\vdots$$a_{n,1}$$a_{n,2}$$\cdots$$a_{n,n}$如上所示的矩阵是一个n阶矩阵,若对于任意的$i,j$,都有$a_{i,j}=a_{j,i}$,则称之为对称矩阵。其中的元素也可以根据i,j的大小分为三个部门:$i=j$主对角线,$i>j$ 下三角区,$i<j$ 上三角区。 普通存储:n*n二维数组,因为上下两个三角区数值相同,所以可以压缩存储。 压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区) 同时我们需要按照行/列优先的原则存入到一个一维数组中,并建立i,j(矩阵下标)与数组下标的映射关系。 以下以行优先为例: 对于i>=j的下标来说,第一个存储的是 i=1,j=1,第二个存储的是 i=2,j=1,接着 2,2、3,1、3,2、3,3。分别映射到了0,1,2,3上面。 根据不难看出,对于i是累加的,比如第一行起始是0,第二行起始是1,到了第三行起始就变为了3。那么其实他就是一个等差数列。 根据等差数列求和公式:$\frac{n(a_1 + a_n)}{2}$,其中$a_1 = 0$,$a_n = i - 1$,$n = i$。因此,第$i$行的起始下标为$\frac{i(i-1)}{2}$。接着我们加上j的偏移量,得到下标为$\frac{i(i-1)}{2} + j - 1$。(j-1的原因是因为数组下标从0开始) 至此我们把矩阵中下三角的元素都存储了,正因为$a_{i,j} = a_{j,i}$,对于上三角的元素,我们直接替换下标即可。 得到最终的下标转换公式如下: $$ k = \begin{cases} \frac{(i-1)i}{2} + j-1, & \text{当 } i \geq j \text{(下三角区和主对角线元素)} \\ \frac{(j-1)j}{2} + i-1, & \text{当 } i < j \text{(上三角区元素)} \end{cases} $$按照上面的方法,分析列优先: 对于i>=j的下标来说,第一个存储的是 i=1,j=1,第二个存储的是 i=1,j=2,接着 2,2、1,3、2,3、3,3。分别映射到了0,1,2,3上面。 根据等差数列求和公式:$\frac{n(a_1 + a_n)}{2}$,其中$a_1 = 0$,$a_n = j - 1$,$n = j$。因此,第$j$列的起始下标为$\frac{j(j-1)}{2}$。接着我们加上i的偏移量,得到下标为$\frac{j(j-1)}{2} + i - 1$。(i-1的原因是因为数组下标从0开始) 至此,我们得到列优先的公式为: $$ k = \begin{cases} \frac{j(j-1)}{2} + i - 1, & \text{if } i \geq j \\ \frac{i(i-1)}{2} + j - 1, & \text{if } i < j \end{cases} $$对于存储上三角的方法,我不想写了,留给我自己思考去吧三角矩阵 $a_{1,1}$$C$$C$$C$$a_{2,1}$$a_{2,2}$$C$$C$$a_{3,1}$$a_{3,2}$$a_{3,3}$$C$$a_{4,1}$$a_{4,2}$$a_{4,3}$$a_{4,4}$下三角矩阵:除了主对角线和下三角区,其余的元素都相同(如表格所示) 上三角矩阵:除了主对角线和上三角区,其余的元素都相同(如表格所示) 压缩存储策略(下三角矩阵为例):按行优先原则将下三角区存入一维数组中。并在最后一个位置存储常量C,上面分析的下三角区存储公式可以直接使用。而常数C的存储位置为$n(n+1)/2$ 存储下三角矩阵的下标转换公式: $$ k = \begin{cases} \frac{(i-1)i}{2} + j - 1, & \ \text{if } i \geq j (下三角区和主对角线元素) \\ \frac{n(n+1)}{2}, & \text{if } i < j (上三角区元素) \end{cases} $$下面开始分析上三角矩阵的存储,还是上面的策略,常数C的存储位置为$n(n+1)/2$。 那么对于第i行应当开始存储的位置应该为上i-1行的元素个数,应当为$n(i-1)-\frac{(i-1)(i-2)}{2}=\frac{(i-1)(2n-i+2)}{2}$,其中,$n(i-1)$代表该矩阵第i行之前一共的元素数目,之后的式子代表下三角区的累计数目,对于第j列,应为相对于对角线的偏移量即为(j-i)。 因此我们可以得到存储上三角矩阵的下标转换公式: $$ k = \begin{cases} \frac{(i-1)(2n-i+2)}{2} + (j-i) & i \leq j (上三角区和主对角线元素) \\ \frac{n(n+1)}{2} & i > j (下三角区元素) \end{cases} $$三对角矩阵 三对角矩阵,又称带状矩阵:当$|i-j|>1$时,元素值为0。$(1\leq i,j\leq n)$ $a_{1,1}$$a_{1,2}$0000$a_{2,1}$$a_{2,2}$$a_{2,3}$0000$a_{3,2}$$a_{3,3}$$a_{3,4}$0000$a_{4,3}$$a_{4,4}$$a_{4,5}$0000$a_{5,4}$$a_{5,5}$$a_{5,6}$0000$a_{6,5}$$a_{6,6}$压缩存储策略:按行优先(或列优先)原则,只存储带状部分 那么按行优先规则,前i-1行的元素个数为$3(i-1)-1$,第i行的元素个数为3,最后一行的元素个数为2。那么$a_{i,j}$是第i行的第j-i+2(如果下标从1开始,从零开始还要减1)个元素。所以我们得到如下的公式: $$ k=3(i-1)-1+j-i+2-1=2i+j-3 $$接下来我们需要讨论一下逆向,即通过k求i和j: 由一维数组下标 $k$ 求矩阵下标 $i, j$ 的方法如下:首先确定行号 $i$,由于前 $i-1$ 行共 $3(i-1)-1$ 个元素,前 $i$ 行共 $3i-1$ 个元素,因此有 $3(i-1)-1 < k+1 \leq 3i-1$,即 $i \geq \frac{k+2}{3}$,向上取整得 $i = \lceil \frac{k+2}{3} \rceil$。 也可以按照王道书的逻辑,$3(i-1)-1 \leq k < 3i-1$,即 $i \leq \frac{k+1}{3} + 1$,向下取整得 $i = \lfloor \frac{k+1}{3} \rfloor + 1$。确定 $i$ 后,前 $i-1$ 行共 $3(i-1)-1$ 个元素,第 $i$ 行的第一个元素下标为 $k_0 = 3(i-1)-1$,所以列号 $j = k - k_0 - 2 + i$。公式总结如下: $$ \begin{aligned} &i = \lceil \frac{k+2}{3} \rceil \\ &j = k - [3(i-1)-1] - 2 + i \end{aligned} $$或者 $$ \begin{aligned} &i = \lfloor \frac{k+1}{3} \rfloor + 1 \\ &j = k - [3(i-1)-1] - 2 + i \end{aligned} $$先根据 $k$ 计算 $i$,再用 $i$ 计算 $j$,两种取整方式结果一致。 稀疏矩阵 稀疏矩阵:非零元素远远少于矩阵元素的个数 压缩存储策略:顺序存储——三元组<行,列,值> 例如,下面的稀疏矩阵: 004005030900000070020000000000其三元组顺序存储形式为:(行、列标从0开始) i行j列v值024055113139247312行、列标从1开始 行列值134165223249357422既然有顺序存储,那么会有链式存储的方式。压缩存储策略二:链式存储——十字链表法 一个结点包含五部分内容:行、列、值、指向下一个同列元素的指针、指向下一个同行元素的指针。 还是上面的矩阵,如果给他创建一个十字链表,那么就会得到如下结果(图源王道课PPT): md1ebaq6.png图片